Advertisements
Advertisements
Question
Find the feasible solution of the following inequation:
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Solution
| Given inequalities | 3x + 2y ≤ 18 | 2x + y ≤ 10 |
| Corresponding equalities | 3x + 2y = 18 | 2x + y = 10 |
| Intersection of line with X-axis | A(6, 0) | C(5, 0) |
| Intersection of line with Y-axis | B(0, 9) | D(0, 10) |
| Origin test |
3(0) + 2(0) ≤ 18 i.e., 0 ≤ 18 which is true |
2(0) + 0 ≤ 10 i.e., 0 ≤ 10 which is true |
| Region | Origin side of the line | Origin side of the line |
x ≥ 0, y ≥ 0 represent 1st quadrant.
The shaded portion represents the feasible solution.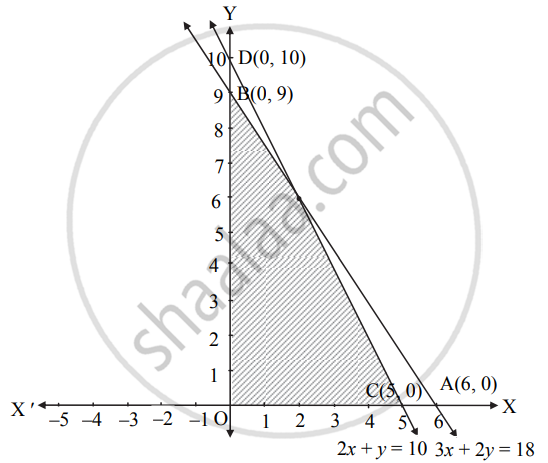
RELATED QUESTIONS
Which of the following statements is correct?
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
Find the feasible solution of the following inequations:
x - 2y ≤ 2, x + y ≥ 3, - 2x + y ≤ 4, x ≥ 0, y ≥ 0
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14. 22 and 1 units of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients:
| Fodder → | Fodder 1 | Fodder 2 |
| Nutrient ↓ | ||
| Nutrients A | 2 | 1 |
| Nutrients B | 2 | 3 |
| Nutrients C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder 2 ₹ 2. Formulate the LPP to minimize the cost.
A company manufactures two types of chemicals Aand B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.
| Chemical→ | A | B | Availability |
| Raw Material ↓ | |||
| P | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. (Assume that the entire production of A and B can be sold). How many units of the chemicals A and B should be manufactured so that the company gets a maximum profit? Formulate the problem as LPP to maximize profit.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
Solve the following LPP by graphical method:
Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Which of the following is correct?
The maximum value of z = 5x + 3y subject to the constraints 3x + 5y ≤ 15, 5x + 2y ≤ 10, x, y ≥ 0 is ______.
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
If the corner points of the feasible solution are (0, 0), (3, 0), (2, 1), `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
Solve the following LPP:
Maximize z = 6x + 10y subject to 3x + 5y ≤ 10, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
Find graphical solution for the following system of linear in equation:
3x + 4y ≤ 12, x - 2y ≥ 2, y ≥ - 1
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II and 2 hours on Machine III. Magazine B requires 3 hours on Machine I, 2 hours on Machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, 60 hours per week respectively. Formulate the Linear programming problem to maximize the profit.
Choose the correct alternative :
Feasible region; the set of points which satify.
Choose the correct alternative :
Solution of LPP to minimize z = 2x + 3y st. x ≥ 0, y ≥ 0, 1≤ x + 2y ≤ 10 is
Choose the correct alternative :
The corner points of the feasible region given by the inequations x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0, are
Fill in the blank :
A dish washing machine holds up to 40 pieces of large crockery (x) This constraint is given by_______.
State whether the following is True or False :
Saina wants to invest at most ₹ 24000 in bonds and fixed deposits. Mathematically this constraints is written as x + y ≤ 24000 where x is investment in bond and y is in fixed deposits.
State whether the following is True or False :
The point (1, 2) is not a vertex of the feasible region bounded by 2x + 3y ≤ 6, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
State whether the following is True or False :
The feasible solution of LPP belongs to only quadrant I.
Maximize z = 10x + 25y subject to x + y ≤ 5, 0 ≤ x ≤ 3, 0 ≤ y ≤ 3
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
The variables involved in LPP are called ______
The constraint that in a particular XII class, number of boys (y) are less than number of girls (x) is given by ______
A company manufactures two models of voltage stabilizers viz., ordinary and auto-cut. All components of the stabilizers are purchased from outside sources, assembly and testing is carried out at the company’s own works. The assembly and testing time required for the two models are 0.8 hours each for ordinary and 1.20 hours each for auto-cut. Manufacturing capacity 720 hours at present is available per week. The market for the two models has been surveyed which suggests a maximum weekly sale of 600 units of ordinary and 400 units of auto-cut. Profit per unit for ordinary and auto-cut models has been estimated at ₹ 100 and ₹ 150 respectively. Formulate the linear programming problem.
A solution which maximizes or minimizes the given LPP is called
The maximum value of the objective function Z = 3x + 5y subject to the constraints x ≥ 0, y ≥ 0 and 2x + 5y ≤ 10 is
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
The values of θ satisfying sin7θ = sin4θ - sinθ and 0 < θ < `pi/2` are ______
Solve the following LP.P.
Maximize z = 13x + 9y,
Subject to 3x + 2y ≤ 12,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
Two kinds of foods A and B are being considered to form a weekly diet. The minimum weekly requirements of fats, Carbohydrates and proteins are 12, 16 and 15 units respectively. One kg of food A has 2, 8 and 5 units respectively of these ingredients and one kg of food B has 6, 2 and 3 units respectively. The price of food A is Rs. 4 per kg and that of food B is Rs. 3 per kg. Formulate the L.P.P. and find the minimum cost.
Sketch the graph of the following inequation in XOY co-ordinate system.
2y - 5x ≥ 0
