Advertisements
Advertisements
Question
Choose the correct alternative :
The corner points of the feasible region given by the inequations x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0, are
Options
(0, 0), (4, 0), (3, 1), (0, 4).
(0, 0), `(7/2, 0)`, (3, 1), (0, 4).
(0, 0), `(7/2, 0), (3, 1)`, (5, 7).
(6, 0), (4, 0), (3, 1), (0, 7).
Solution
Given inequalities are x + y ≤ 4, 2x + y ≤ 7.
Consider line L1 : x + y = 4 and L2 : 2x + y = 7
For line L1, A (0, 4) and B (4, 0)
For line L2, P(0, 7) and Q`(7/2, 0)`
Solving both lines, we get x = 3, y = 1.
The coordinates of origin O (0, 0) satisfies both the inequalities.
∴ The required region is on the origin side of both the lines L1 and L2.
As x ≥ 0, y ≥ 0, the feasible region is in the first quadrant.
OQRAO is the required feasible region.
∴ The corner points are O (0, 0), Q`(7/2, 0)`, R (3, 1), A (0, 4).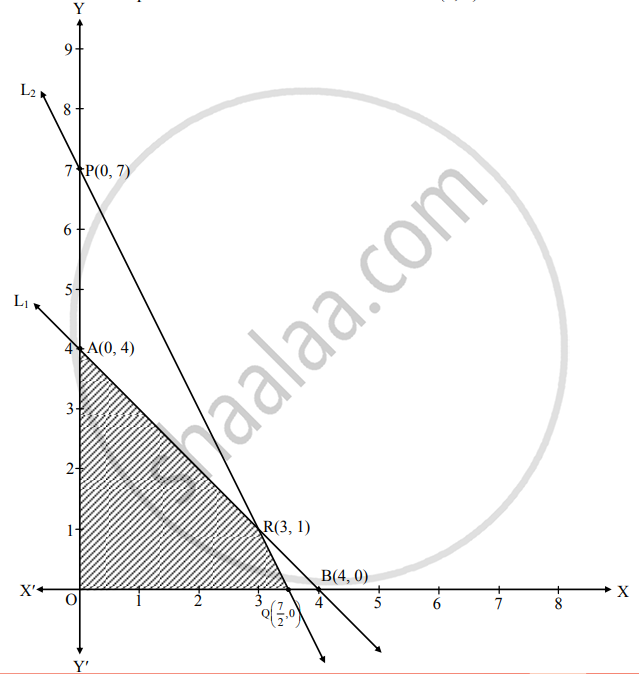
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequation:
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find feasible solution graphically.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
Solution of LPP to minimize z = 2x + 3y, such that x ≥ 0, y ≥ 0, 1 ≤ x + 2y ≤ 10 is ______.
Solve the following LPP:
Maximize z = 6x + 10y subject to 3x + 5y ≤ 10, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
Solve each of the following inequations graphically using XY-plane:
- 11x - 55 ≤ 0
A company produces mixers and food processors. Profit on selling one mixer and one food processor is Rs 2,000 and Rs 3,000 respectively. Both the products are processed through three machines A, B, C. The time required in hours for each product and total time available in hours per week on each machine arc as follows:
| Machine | Mixer | Food Processor | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced in order to maximize the profit?
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to machine shop for finishing. The number of man hours of labour required in each shop for production of A and B and the number of man hours available for the firm are as follows:
| Gadgets | Foundry | Machine Shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hours) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per unit. Formulate the L.P.P. to have maximum profit.
A company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the table below:
| Raw Material\Fertilizers | F1 | F2 | Availability |
| A | 2 | 3 | 40 |
| B | 1 | 4 | 70 |
By selling one unit of F1 and one unit of F2, company gets a profit of ₹ 500 and ₹ 750 respectively. Formulate the problem as L.P.P. to maximize the profit.
Fill in the blank :
A dish washing machine holds up to 40 pieces of large crockery (x) This constraint is given by_______.
Minimize z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
x − y ≤ 1, x − y ≥ 0, x ≥ 0, y ≥ 0 are the constant for the objective function z = x + y. It is solvable for finding optimum value of z? Justify?
State whether the following statement is True or False:
LPP is related to efficient use of limited resources
Solve the following linear programming problems by graphical method.
Minimize Z = 20x1 + 40x2 subject to the constraints 36x1 + 6x2 ≥ 108; 3x1 + 12x2 ≥ 36; 20x1 + 10x2 ≥ 100 and x1, x2 ≥ 0.
In the given graph the coordinates of M1 are

A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
The LPP to maximize Z = x + y, subject to x + y ≤ 1, 2x + 2y ≥ 6, x ≥ 0, y ≥ 0 has ________.
The maximum value of Z = 9x + 13y subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is ______.
For the following shaded region, the linear constraint are: