Advertisements
Advertisements
Question
Solve the following linear programming problems by graphical method.
Minimize Z = 20x1 + 40x2 subject to the constraints 36x1 + 6x2 ≥ 108; 3x1 + 12x2 ≥ 36; 20x1 + 10x2 ≥ 100 and x1, x2 ≥ 0.
Solution
Given that 36x1 + 6x2 ≥ 108
Let 36x1 + 6x2 = 108
6x1 + x2 = 18
| x1 | 0 | 3 | 2 |
| x2 | 18 | 0 | 6 |
Also given that 3x1 + 12x2 ≥ 36
Let 3x1 + 12x2 = 36
x1 + 4x2 = 12
| x1 | 0 | 12 | 4 |
| x2 | 3 | 0 | 2 |
Also given that 20x1 + 10x2 ≥ 100
Let 20x1 + 10x2 = 100
2x1 + x2 = 10
| x1 | 0 | 5 | 4 |
| x2 | 10 | 0 | 2 |
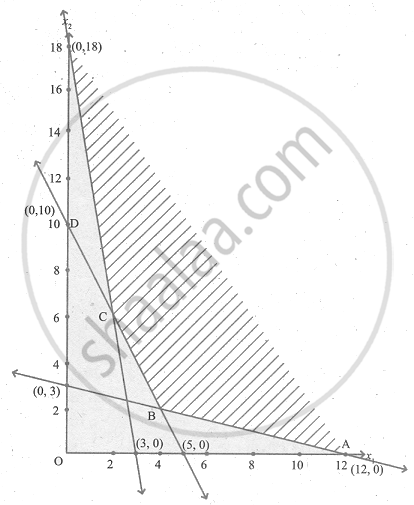
The feasible region satisfying all the conditions is ABCD.
The coordinates of the comer points are A(12, 0), B(4, 2), C(2, 6) and D(0, 18).
| Corner points | Z = 20x1 + 40x2 |
| A(12, 0) | 240 |
| B(4, 2) | 80 + 80 = 160 |
| C(2, 6) | 40 + 240 = 280 |
| D(0, 18) | 720 |
The minimum value of Z occurs at B(4, 2)
∴ The optimal solution is x1 = 4, x2 = 2 and Zmin = 160
APPEARS IN
RELATED QUESTIONS
Which of the following statements is correct?
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for production of A and B per unit and the number of man-hours available for the firm is as follows :
| Gadgets | Foundry | Machine shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hour) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Solve the following LPP by graphical method:
Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
In the given graph the coordinates of M1 are

Given an L.P.P maximize Z = 2x1 + 3x2 subject to the constrains x1 + x2 ≤ 1, 5x1 + 5x2 ≥ 0 and x1 ≥ 0, x2 ≥ 0 using graphical method, we observe
The point which provides the solution of the linear programming problem, Max.(45x + 55y) subject to constraints x, y ≥ 0, 6x + 4y ≤ 120, 3x + 10y ≤ 180, is ______
The maximum value of Z = 9x + 13y subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is ______.
Sketch the graph of the following inequation in XOY co-ordinate system.
x + y ≤ 0
