Advertisements
Advertisements
प्रश्न
Solve the following linear programming problems by graphical method.
Minimize Z = 20x1 + 40x2 subject to the constraints 36x1 + 6x2 ≥ 108; 3x1 + 12x2 ≥ 36; 20x1 + 10x2 ≥ 100 and x1, x2 ≥ 0.
उत्तर
Given that 36x1 + 6x2 ≥ 108
Let 36x1 + 6x2 = 108
6x1 + x2 = 18
| x1 | 0 | 3 | 2 |
| x2 | 18 | 0 | 6 |
Also given that 3x1 + 12x2 ≥ 36
Let 3x1 + 12x2 = 36
x1 + 4x2 = 12
| x1 | 0 | 12 | 4 |
| x2 | 3 | 0 | 2 |
Also given that 20x1 + 10x2 ≥ 100
Let 20x1 + 10x2 = 100
2x1 + x2 = 10
| x1 | 0 | 5 | 4 |
| x2 | 10 | 0 | 2 |
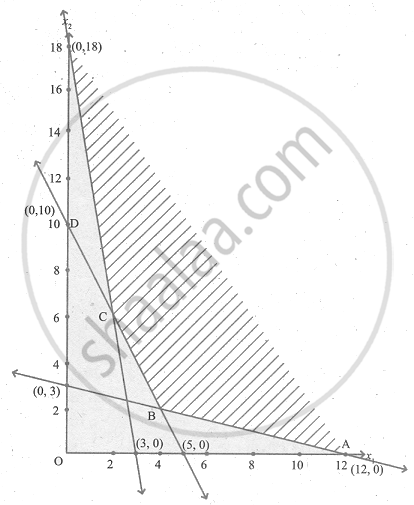
The feasible region satisfying all the conditions is ABCD.
The coordinates of the comer points are A(12, 0), B(4, 2), C(2, 6) and D(0, 18).
| Corner points | Z = 20x1 + 40x2 |
| A(12, 0) | 240 |
| B(4, 2) | 80 + 80 = 160 |
| C(2, 6) | 40 + 240 = 280 |
| D(0, 18) | 720 |
The minimum value of Z occurs at B(4, 2)
∴ The optimal solution is x1 = 4, x2 = 2 and Zmin = 160
APPEARS IN
संबंधित प्रश्न
Find the feasible solution of the following inequation:
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
The corner points of the feasible solution given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0 are ______.
Fill in the blank :
The optimal value of the objective function is attained at the _______ points of feasible region.
A train carries at least twice as many first class passengers (y) as second class passengers (x) The constraint is given by_______
Fill in the blank :
A dish washing machine holds up to 40 pieces of large crockery (x) This constraint is given by_______.
A company produces two types of products say type A and B. Profits on the two types of product are ₹ 30/- and ₹ 40/- per kg respectively. The data on resources required and availability of resources are given below.
| Requirements | Capacity available per month | ||
| Product A | Product B | ||
| Raw material (kgs) | 60 | 120 | 12000 |
| Machining hours/piece | 8 | 5 | 600 |
| Assembling (man hours) | 3 | 4 | 500 |
Formulate this problem as a linear programming problem to maximize the profit.
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
The minimum value of the objective function Z = x + 3y subject to the constraints 2x + y ≤ 20, x + 2y ≤ 20, x > 0 and y > 0 is
Sketch the graph of the following inequation in XOY co-ordinate system.
2y - 5x ≥ 0
