Advertisements
Advertisements
प्रश्न
Find the feasible solution of the following inequation:
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
उत्तर
First we draw the lines AB, CD and EF whose equations are x + 4y = 24, 3x + y = 21 and x + y = 9 respectively.
| Line | Equation | Points on the X-axis | Points on the Y-axis | Sign | Region |
| AB | x + 4y = 24 | A (24,0) | B (0,6) | ≤ | origin side of line AB |
| CB | 3x + y = 21 | C (7,0) | D(0,21) | ≤ | origin side of line CD |
| EF | x + y = 9 | E(9,0) | F(0,9) | ≤ | origin side of line EF |
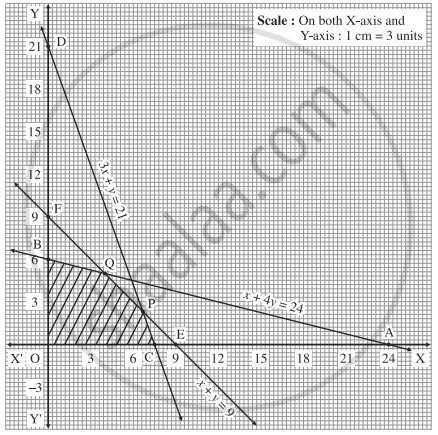
The feasible solution is OCPQBO which is shaded in the graph.
APPEARS IN
संबंधित प्रश्न
Find the feasible solution of the following inequation:
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Find the feasible solution of the following inequation:
3x + 4y ≥ 12, 4x + 7y ≤ 28, y ≥ 1, x ≥ 0.
If John drives a car at a speed of 60 km/hour, he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 km/hour, the cost of petrol increases ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Solve the following LPP by graphical method:
Maximize z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Solve the following LPP by graphical method:
Minimize z = 8x + 10y, subject to 2x + y ≥ 7, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0.
Select the appropriate alternatives for each of the following question:
The value of objective function is maximum under linear constraints
The maximum value of z = 5x + 3y subject to the constraints 3x + 5y ≤ 15, 5x + 2y ≤ 10, x, y ≥ 0 is ______.
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
Solution of LPP to minimize z = 2x + 3y, such that x ≥ 0, y ≥ 0, 1 ≤ x + 2y ≤ 10 is ______.
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
Find graphical solution for the following system of linear in equation:
3x + 4y ≤ 12, x - 2y ≥ 2, y ≥ - 1
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
A firm manufactures two products A and B on which profit earned per unit ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. The product A requires one minute of processing time on M1 and two minutes of processing time on M2, B requires one minute of processing time on M1 and one minute of processing time on M2. Machine M1 is available for use for 450 minutes while M2 is available for 600 minutes during any working day. Find the number of units of product A and B to be manufactured to get the maximum profit.
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to machine shop for finishing. The number of man hours of labour required in each shop for production of A and B and the number of man hours available for the firm are as follows:
| Gadgets | Foundry | Machine Shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hours) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per unit. Formulate the L.P.P. to have maximum profit.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B.
| Raw Material \Chemical | A | B | Availability |
| p | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. Formulate the problem as L.P.P. to maximize the profit.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II and 2 hours on Machine III. Magazine B requires 3 hours on Machine I, 2 hours on Machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, 60 hours per week respectively. Formulate the Linear programming problem to maximize the profit.
Choose the correct alternative :
Of all the points of the feasible region the optimal value of z is obtained at a point
Choose the correct alternative :
Solution of LPP to minimize z = 2x + 3y st. x ≥ 0, y ≥ 0, 1≤ x + 2y ≤ 10 is
Choose the correct alternative :
The corner points of the feasible region given by the inequations x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0, are
If the corner points of the feasible region are (0, 0), (3, 0), (2, 1) and `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
State whether the following is True or False :
The feasible solution of LPP belongs to only quadrant I.
The point of which the maximum value of z = x + y subject to constraints x + 2y ≤ 70, 2x + y ≤ 90, x ≥ 0, y ≥ 0 is obtained at
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Minimize z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
Choose the correct alternative:
The feasible region is
State whether the following statement is True or False:
Objective function of LPP is a relation between the decision variables
State whether the following statement is True or False:
LPP is related to efficient use of limited resources
Solve the following linear programming problems by graphical method.
Minimize Z = 3x1 + 2x2 subject to the constraints 5x1 + x2 ≥ 10; x1 + x2 ≥ 6; x1 + 4x2 ≥ 12 and x1, x2 ≥ 0.
A solution which maximizes or minimizes the given LPP is called
In the given graph the coordinates of M1 are

Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
The values of θ satisfying sin7θ = sin4θ - sinθ and 0 < θ < `pi/2` are ______
Find graphical solution for the following system of linear in equation:
x + 2y ≥ 4, 2x - y ≤ 6
