Advertisements
Advertisements
प्रश्न
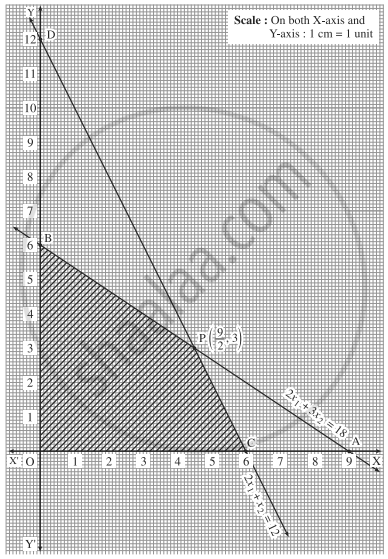
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
उत्तर
First we draw the lines AB and CD whose equations are 2x1 + 3x2 = 18 and 2x1 + x2 = 12 respectively.
| Line | Equation | Points on the X-axis | Points on the Y-axis | Sign | Region |
| AB | 2x1 + 3x2 = 18 | A(9, 0) | B(0, 6) | ≤ | origin side of line AB |
| CD | 2x1 + x2 = 12 | C(6, 0) | O(0, 12) | ≤ | origin side of line CD |
The feasible region is OCPBO which is shaded in the graph. The vertices of the feasible region are O (0, 0), C (6, 0), P and B (0, 6).
P is the point of intersection of the lines
2x1 + 3x2 = 18 ....(1)
and 2x1 + x2 = 12 ....(2)
On subtracting, we get
2x2 = 6
∴ x2 = 3
Substituting x2 = 3 in (2), we get
2x1 + 3 = 12
∴ x1 = 9
∴ P is `(9/2, 3)`
The values of objective function z = 5x1 + 6x2 at these vertices are
z(O) = 5(0) + 6(0) = 0 + 0 = 0
z(C) = 5(6) + 6(0) = 30 + 0 = 30
z(P) = `5(9/2) + 6(3) = 45/2 + 18 = (45 + 36)/2 = 81/2 = 40.5`
z(B) = 5(0) + 6(3) = 0 + 18 = 18
Maximum value of z is 40.5 when x1 = `9/2` y1 = 3.
APPEARS IN
संबंधित प्रश्न
Which of the following statements is correct?
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for production of A and B per unit and the number of man-hours available for the firm is as follows :
| Gadgets | Foundry | Machine shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hour) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14. 22 and 1 units of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients:
| Fodder → | Fodder 1 | Fodder 2 |
| Nutrient ↓ | ||
| Nutrients A | 2 | 1 |
| Nutrients B | 2 | 3 |
| Nutrients C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder 2 ₹ 2. Formulate the LPP to minimize the cost.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
Solve the following LPP by graphical method:
Maximize z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Solve the following LPP by graphical method:
Minimize z = 8x + 10y, subject to 2x + y ≥ 7, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0.
Which of the following is correct?
Objective function of LPP is ______.
The maximum value of z = 5x + 3y subject to the constraints 3x + 5y ≤ 15, 5x + 2y ≤ 10, x, y ≥ 0 is ______.
The corner points of the feasible solution are (0, 0), (2, 0), `(12/7, 3/7)`, (0, 1). Then z = 7x + y is maximum at ______.
If the corner points of the feasible solution are (0, 0), (3, 0), (2, 1), `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
Solve the following LPP:
Maximize z = 6x + 10y subject to 3x + 5y ≤ 10, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
A company produces mixers and food processors. Profit on selling one mixer and one food processor is Rs 2,000 and Rs 3,000 respectively. Both the products are processed through three machines A, B, C. The time required in hours for each product and total time available in hours per week on each machine arc as follows:
| Machine | Mixer | Food Processor | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced in order to maximize the profit?
A chemical company produces a chemical containing three basic elements A, B, C, so that it has at least 16 litres of A, 24 litres of B and 18 litres of C. This chemical is made by mixing two compounds I and II. Each unit of compound I has 4 litres of A, 12 litres of B and 2 litres of C. Each unit of compound II has 2 litres of A, 2 litres of B and 6 litres of C. The cost per unit of compound I is ₹ 800 and that of compound II is ₹ 640. Formulate the problems as LPP and solve it to minimize the cost.
Fill in the blank :
A dish washing machine holds up to 40 pieces of large crockery (x) This constraint is given by_______.
State whether the following is True or False :
Saina wants to invest at most ₹ 24000 in bonds and fixed deposits. Mathematically this constraints is written as x + y ≤ 24000 where x is investment in bond and y is in fixed deposits.
Maximize z = 5x + 2y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Maximize z = −x + 2y subjected to constraints x + y ≥ 5, x ≥ 3, x + 2y ≥ 6, y ≥ 0 is this LPP solvable? Justify your answer.
Choose the correct alternative:
Z = 9x + 13y subjected to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, 0 ≤ x, y was found to be maximum at the point
State whether the following statement is True or False:
LPP is related to efficient use of limited resources
Constraints are always in the form of ______ or ______.
A company manufactures two models of voltage stabilizers viz., ordinary and auto-cut. All components of the stabilizers are purchased from outside sources, assembly and testing is carried out at the company’s own works. The assembly and testing time required for the two models are 0.8 hours each for ordinary and 1.20 hours each for auto-cut. Manufacturing capacity 720 hours at present is available per week. The market for the two models has been surveyed which suggests a maximum weekly sale of 600 units of ordinary and 400 units of auto-cut. Profit per unit for ordinary and auto-cut models has been estimated at ₹ 100 and ₹ 150 respectively. Formulate the linear programming problem.
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
A solution which maximizes or minimizes the given LPP is called
In the given graph the coordinates of M1 are

A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
The minimum value of z = 5x + 13y subject to constraints 2x + 3y ≤ 18, x + y ≥ 10, x ≥ 0, y ≥ 2 is ______
The point which provides the solution of the linear programming problem, Max.(45x + 55y) subject to constraints x, y ≥ 0, 6x + 4y ≤ 120, 3x + 10y ≤ 180, is ______
Shamli wants to invest ₹ 50, 000 in saving certificates and PPF. She wants to invest atleast ₹ 15,000 in saving certificates and at least ₹ 20,000 in PPF. The rate of interest on saving certificates is 8% p.a. and that on PPF is 9% p.a. Formulation of the above problem as LPP to determine maximum yearly income, is ______.
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y Subject to: x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
Sketch the graph of the following inequation in XOY co-ordinate system.
x + y ≤ 0
Sketch the graph of the following inequation in XOY co-ordinate system.
2y - 5x ≥ 0
