Advertisements
Advertisements
प्रश्न
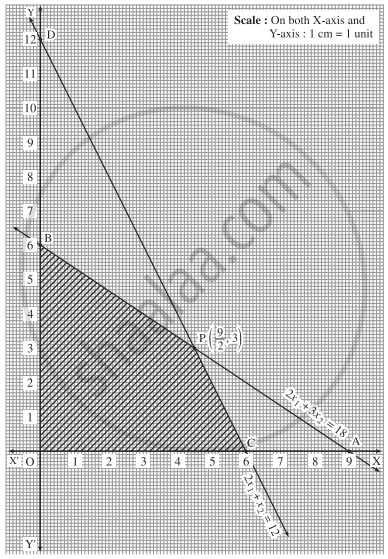
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
उत्तर
First we draw the lines AB and CD whose equations are 2x1 + 3x2 = 18 and 2x1 + x2 = 12 respectively.
| Line | Equation | Points on the X-axis | Points on the Y-axis | Sign | Region |
| AB | 2x1 + 3x2 = 18 | A(9, 0) | B(0, 6) | ≤ | origin side of line AB |
| CD | 2x1 + x2 = 12 | C(6, 0) | O(0, 12) | ≤ | origin side of line CD |
The feasible region is OCPBO which is shaded in the graph. The vertices of the feasible region are O (0, 0), C (6, 0), P and B (0, 6).
P is the point of intersection of the lines
2x1 + 3x2 = 18 ....(1)
and 2x1 + x2 = 12 ....(2)
On subtracting, we get
2x2 = 6
∴ x2 = 3
Substituting x2 = 3 in (2), we get
2x1 + 3 = 12
∴ x1 = 9
∴ P is `(9/2, 3)`
The values of objective function z = 5x1 + 6x2 at these vertices are
z(O) = 5(0) + 6(0) = 0 + 0 = 0
z(C) = 5(6) + 6(0) = 30 + 0 = 30
z(P) = `5(9/2) + 6(3) = 45/2 + 18 = (45 + 36)/2 = 81/2 = 40.5`
z(B) = 5(0) + 6(3) = 0 + 18 = 18
Maximum value of z is 40.5 when x1 = `9/2` y1 = 3.
APPEARS IN
संबंधित प्रश्न
Find the feasible solution of the following inequations:
x - 2y ≤ 2, x + y ≥ 3, - 2x + y ≤ 4, x ≥ 0, y ≥ 0
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 in magazines A and B per copy. These are processed on three Machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II, and 2 hours on machine III. Magazine B requires 3 hours on machine I, 2 hours on machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, and 60 hours per week respectively. Formulate the LPP to determine weekly production of magazines A and B, so that the total profit is maximum.
If John drives a car at a speed of 60 km/hour, he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 km/hour, the cost of petrol increases ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
Minimize z = 6x + 2y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Objective function of LPP is ______.
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
The point of which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x, ≥ 0, y ≥ 0 is is obtained at ______.
Of all the points of the feasible region, the optimal value of z obtained at the point lies ______.
The corner points of the feasible solution are (0, 0), (2, 0), `(12/7, 3/7)`, (0, 1). Then z = 7x + y is maximum at ______.
If the corner points of the feasible solution are (0, 10), (2, 2) and (4, 0), then the point of minimum z = 3x + 2y is ______.
Solve the following LPP:
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0.
Solve each of the following inequations graphically using XY-plane:
4x - 18 ≥ 0
Solve the following LPP:
Minimize z = 4x + 2y
Subject to 3x + y ≥ 27, x + y ≥ 21, x + 2y ≥ 30, x ≥ 0, y ≥ 0
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each units of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufactured per month to maximize profit? How much is the maximum profit?
A company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the table below:
| Raw Material\Fertilizers | F1 | F2 | Availability |
| A | 2 | 3 | 40 |
| B | 1 | 4 | 70 |
By selling one unit of F1 and one unit of F2, company gets a profit of ₹ 500 and ₹ 750 respectively. Formulate the problem as L.P.P. to maximize the profit.
Choose the correct alternative :
Of all the points of the feasible region the optimal value of z is obtained at a point
Choose the correct alternative :
Feasible region; the set of points which satify.
Fill in the blank :
“A gorage employs eight men to work in its shownroom and repair shop. The constraints that there must be at least 3 men in showroom and at least 2 men in repair shop are ______ and _______ respectively.
Fill in the blank :
A dish washing machine holds up to 40 pieces of large crockery (x) This constraint is given by_______.
State whether the following is True or False :
Saina wants to invest at most ₹ 24000 in bonds and fixed deposits. Mathematically this constraints is written as x + y ≤ 24000 where x is investment in bond and y is in fixed deposits.
State whether the following is True or False :
The point (1, 2) is not a vertex of the feasible region bounded by 2x + 3y ≤ 6, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
State whether the following is True or False :
The feasible solution of LPP belongs to only quadrant I.
The point of which the maximum value of z = x + y subject to constraints x + 2y ≤ 70, 2x + y ≤ 90, x ≥ 0, y ≥ 0 is obtained at
Choose the correct alternative:
The feasible region is
State whether the following statement is True or False:
LPP is related to efficient use of limited resources
The constraint that in a particular XII class, number of boys (y) are less than number of girls (x) is given by ______
A company produces two types of products say type A and B. Profits on the two types of product are ₹ 30/- and ₹ 40/- per kg respectively. The data on resources required and availability of resources are given below.
| Requirements | Capacity available per month | ||
| Product A | Product B | ||
| Raw material (kgs) | 60 | 120 | 12000 |
| Machining hours/piece | 8 | 5 | 600 |
| Assembling (man hours) | 3 | 4 | 500 |
Formulate this problem as a linear programming problem to maximize the profit.
A solution which maximizes or minimizes the given LPP is called
Given an L.P.P maximize Z = 2x1 + 3x2 subject to the constrains x1 + x2 ≤ 1, 5x1 + 5x2 ≥ 0 and x1 ≥ 0, x2 ≥ 0 using graphical method, we observe
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y Subject to: x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
Sketch the graph of the following inequation in XOY co-ordinate system.
2y - 5x ≥ 0
