Advertisements
Advertisements
प्रश्न
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
उत्तर
Maximise Z = 4x1 + x2
Subject to the constraints
x1 + x2 ≤ 50
3x1 + x2 ≤ 90
x1, x2 ≥ 0
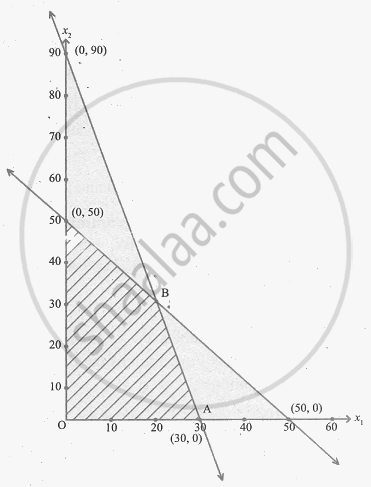
Since the decision variables, x1 and x2 are non-negative, the solution lies in the I quadrant of the plane.
Consider the equations
x1 + x2 = 50
| x1 | 0 | 50 |
| x2 | 50 | 0 |
3x1 + x2 = 90
| x1 | 0 | 30 |
| x2 | 90 | 0 |
The feasible region is OABC and its co-ordinates are O(0, 0) A(30, 0) C(0, 50) and B is the point of intersection of the lines
x1 + x2 = 50 ..........(1)
and 3x1 + x2 = 90 .........(2)
Verification of B:
x1 + x2 = 50 ..........(1)
3x1 + x2 = 90 .........(2)
− − −
− 2x1 = − 40
x1 = 20
From (1), 20 + x2 = 50
x2 = 30
∴ B is (20, 30)
| Corner points | Z = 4x1 + x2 |
| O(0, 0) | 0 |
| A(30, 0) | 120 |
| B(20, 30) | 110 |
| C(0, 50) | 50 |
Maximum value occurs at A(30, 0)
Hence the solution is x1 = 30, x2 = 0 and Zmax = 120.
APPEARS IN
संबंधित प्रश्न
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for production of A and B per unit and the number of man-hours available for the firm is as follows :
| Gadgets | Foundry | Machine shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hour) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
Solve the following LPP by graphical method:
Maximize z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
The corner points of the feasible solution are (0, 0), (2, 0), `(12/7, 3/7)`, (0, 1). Then z = 7x + y is maximum at ______.
Solve the following LPP:
Maximize z = 2x + 3y subject to x - y ≥ 3, x ≥ 0, y ≥ 0.
Maximize z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
x − y ≤ 1, x − y ≥ 0, x ≥ 0, y ≥ 0 are the constant for the objective function z = x + y. It is solvable for finding optimum value of z? Justify?
A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
The optimal value of the objective function is attained at the ______ of feasible region.
For the following shaded region, the linear constraint are: