Advertisements
Advertisements
प्रश्न
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
उत्तर
Since the decision variables, x1 and x2 are non-negative, the solution lies in the I quadrant of the plane.
Consider the equations
x1 + x2 = 6
| x1 | 0 | 6 |
| x2 | 6 | 0 |
x1 = 4 is a line parallel to x2-axis at a distance of 4 units.
x2 = 5 is a line parallel to x1-axis at a distance of 5 units.
The feasible region is OABCD and its co-ordinates are O(0, 0) A(4, 0) D(5, 0) and B is the point of intersection of the lines x1 + x2 = 6 and x1 = 4
Also C is the point of intersection of the lines x1 + x2 = 6 and x2 = 5
Verification of B:
x1 + x2 = 6 and x1 = 4
4 + x2 = 6
x2 = 2
∴ B is (4, 2)
Verification of C:
x1 + x2 = 6 and x2 = 5
x1 + 5 = 6
x1 = 1
∴ C is (1, 5)
| Corner points | Z = 3x1 + 5x2 |
| O(0, 0) | 0 |
| A(4, 0) | 12 |
| B(4, 2) | 22 |
| C(1, 5) | 26 |
| D(5, 0) | 15 |
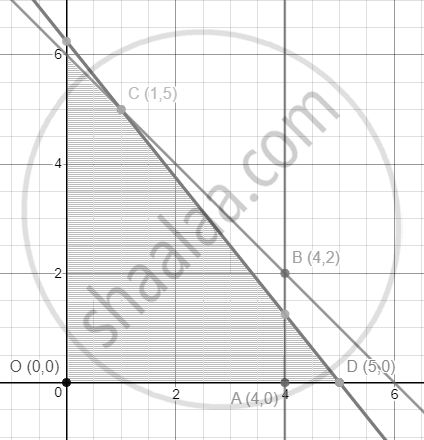
Maximum of Z occurs at C(1, 5)
∴ The solution is x1 = 1, x2 = 5 and Zmax = 26.
APPEARS IN
संबंधित प्रश्न
A furniture dealer deals in tables and chairs. He has ₹ 1,50,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 1500 and a chair ₹ 750. Construct the inequations and find the feasible solution.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Which of the following is correct?
Objective function of LPP is ______.
The corner points of the feasible solution are (0, 0), (2, 0), `(12/7, 3/7)`, (0, 1). Then z = 7x + y is maximum at ______.
Find graphical solution for the following system of linear in equation:
3x + 4y ≤ 12, x - 2y ≥ 2, y ≥ - 1
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II and 2 hours on Machine III. Magazine B requires 3 hours on Machine I, 2 hours on Machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, 60 hours per week respectively. Formulate the Linear programming problem to maximize the profit.
State whether the following is True or False :
The point (1, 2) is not a vertex of the feasible region bounded by 2x + 3y ≤ 6, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
