Advertisements
Advertisements
प्रश्न
A company produces mixers and food processors. Profit on selling one mixer and one food processor is Rs 2,000 and Rs 3,000 respectively. Both the products are processed through three machines A, B, C. The time required in hours for each product and total time available in hours per week on each machine arc as follows:
| Machine | Mixer | Food Processor | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced in order to maximize the profit?
उत्तर
Let x = number of mixers are sold
y = number of food processors are sold
Profit function z = 2000x + 3000y
This is the objective function which is to be maximized. From the given table in the problem, the constraints are
3x + 3y ≤ 36 (above machine A)
5x 2y ≤ 50 ( about machine B)
2x + 6y ≤ 60 ( about machine C)
As the number of mixers and food processors are non-negative.
x ≥ 0, y ≥ 0
Mathematical model of L.P.P. is
Maximize Z = 2000x + 3000y Subject to
3x + 3y ≤ 36, 5x 2y ≤ 50, 2x + 6y ≤ 60
and x ≥ 0, y ≥ 0
First we draw the lines AB, CD and EF whose equations are 3x + 3y = 36, 5x + 2y = 50 and 2x + 6y = 60 respectively.
| Line | Equation | Points on the X-axis | Points on the Y-axis | Sign | Region |
| AB | 3x + 3y = 36 | A(12,0) | B(0,12) | ≤ | origin side of line AB |
| CD | 5x + 2y = 50 | C(10,0) | D(0,25) | ≤ | origin side of line CD |
| EF | 2x + 6y = 60 | E(30,0) | F(0,10) | ≤ | origin side of line EF |
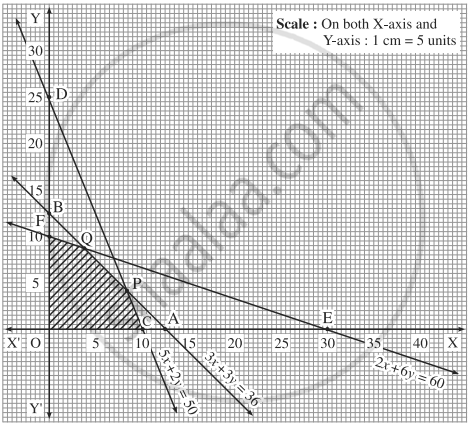
The feasible region is OCPQFO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (10, 0), P, Q and F (0, 10).
P is the point of intersection of the lines
3x + 3y = 36 ....(1)
and 5x + 2y = 50 ....(2)
Multiplying equation (1) by 2 and equation (2) by 3, we get,
6x + 6y = 72
15x + 6y = 150
On subtracting, we get
9x = 78
∴ x = `26/3`
∴ from (1), `3(26/3) + 3"y" = 36`
∴ 3y = 10
∴ y = `10/3`
∴ P = `(26/3,10/3)`
Q is the point of intersection of the lines
3x + 3y = 36 . ...(1)
and 2x + 6y = 60 ...(2)
Multiplying equation (1) by 2, we get
6x + 6y = 72
Subtracting equation (3), from this equation, we get
4x = 12
∴ x = 3
∴ from (1), 3(3) + 3y = 36
∴ 3y = 27
∴ y = 9
∴ Q = (3, 9)
The values of the objective function z = 2000x + 3000y at these vertices are
z(O) = 2000(0) + 3000(0) = 0 + 0 = 0
z(C) = 2000(10) + 3000(0) = 20000 + 0 = 20000
z(P) = `2000(26/3) + 3000(10/3) = 52000/3 + 30000/3 = 82000/3`
z(Q) = 2000(3) + 3000(9) = 6000 + 27000 = 33000
z(F) = 2000(0) + 3000(10) = 30000 + 0 = 30000
∴ the maximum value of z is 33000 at the point (3, 9).
Hence, 3 mixers and 9 food processors should be produced in order to get the maximum profit of ₹ 33,000.
APPEARS IN
संबंधित प्रश्न
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find feasible solution graphically.
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for production of A and B per unit and the number of man-hours available for the firm is as follows :
| Gadgets | Foundry | Machine shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hour) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
A company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the table below:
| Fertilizers→ | F1 | F2 | Availability |
| Raw Material ↓ | |||
| A | 2 | 3 | 40 |
| B | 1 | 4 | 70 |
By selling one unit of F1 and one unit of F2, the company gets a profit of ₹ 500 and ₹ 750 respectively. Formulate the problem as LPP to maximize the profit.
Solve the following LPP by graphical method:
Maximize z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Solve the following LPP by graphical method:
Minimize z = 8x + 10y, subject to 2x + y ≥ 7, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0.
Objective function of LPP is ______.
The corner points of the feasible solution given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0 are ______.
If the corner points of the feasible solution are (0, 0), (3, 0), (2, 1), `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
Solve each of the following inequations graphically using XY-plane:
- 11x - 55 ≤ 0
A chemical company produces a chemical containing three basic elements A, B, C, so that it has at least 16 litres of A, 24 litres of B and 18 litres of C. This chemical is made by mixing two compounds I and II. Each unit of compound I has 4 litres of A, 12 litres of B and 2 litres of C. Each unit of compound II has 2 litres of A, 2 litres of B and 6 litres of C. The cost per unit of compound I is ₹ 800 and that of compound II is ₹ 640. Formulate the problems as LPP and solve it to minimize the cost.
A firm manufactures two products A and B on which profit earned per unit ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. The product A requires one minute of processing time on M1 and two minutes of processing time on M2, B requires one minute of processing time on M1 and one minute of processing time on M2. Machine M1 is available for use for 450 minutes while M2 is available for 600 minutes during any working day. Find the number of units of product A and B to be manufactured to get the maximum profit.
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to machine shop for finishing. The number of man hours of labour required in each shop for production of A and B and the number of man hours available for the firm are as follows:
| Gadgets | Foundry | Machine Shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hours) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per unit. Formulate the L.P.P. to have maximum profit.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B.
| Raw Material \Chemical | A | B | Availability |
| p | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. Formulate the problem as L.P.P. to maximize the profit.
Choose the correct alternative :
Which of the following is correct?
Objective function of LPP is ______.
Choose the correct alternative :
The corner points of the feasible region given by the inequations x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0, are
Choose the correct alternative :
The half plane represented by 3x + 2y ≤ 0 constraints the point.
Choose the correct alternative :
The half plane represented by 4x + 3y ≥ 14 contains the point
A train carries at least twice as many first class passengers (y) as second class passengers (x) The constraint is given by_______
State whether the following is True or False :
The feasible solution of LPP belongs to only quadrant I.
The feasible region is the set of point which satisfy.
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Maximize z = 5x + 2y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Maximize z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
Minimize z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
Choose the correct alternative:
The feasible region is
A company produces two types of pens A and B. Pen A is of superior quality and pen B is of lower quality. Profits on pens A and B are ₹ 5 and ₹ 3 per pen respectively. Raw materials required for each pen A is twice as that of pen B. The supply of raw material is sufficient only for 1000 pens per day. Pen A requires a special clip and only 400 such clips are available per day. For pen B, only 700 clips are available per day. Formulate this problem as a linear programming problem.
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
The values of θ satisfying sin7θ = sin4θ - sinθ and 0 < θ < `pi/2` are ______
The minimum value of z = 5x + 13y subject to constraints 2x + 3y ≤ 18, x + y ≥ 10, x ≥ 0, y ≥ 2 is ______
Food F1 contains 2, 6, 1 units and food F2 contains 1, 1, 3 units of proteins, carbohydrates, fats respectively per kg. 8, 12 and 9 units of proteins, carbohydrates and fats is the weekly minimum requirement for a person. The cost of food F1 is Rs. 85 and food F2 is Rs. 40 per kg. Formulate the L.P.P. to minimize the cost.
