Advertisements
Advertisements
प्रश्न
Minimize z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
उत्तर
To draw the feasible region, construct table as follows:
| Inequality | x + 2y ≥ 3 | x + 4y ≥ 4 | 3x + y ≥ 3 |
| Corresponding equation (of line) | x + 2y = 3 | x + 4y = 4 | 3x + y = 3 |
| Intersection of line with X-axis | (3, 0) | (4, 0) | (1, 0) |
| Intersection of line with Y-axis | `(0, 3/2)` | (0, 1) | (0, 3) |
| Region | Non-origin side | Non-origin side | Non-origin side |
x ≥ 0, y ≥ 0 represent 1st quadrant.
Shaded portion XABCDY is the feasible region, whose vertices are A(4, 0), B, C and D(0, 3).
B is the point of intersection of the lines x + 4y = 4 and x + 2y = 3.
Solving the above equations, we get
x = 2, y = `1/2`
∴ B ≡ `(2, 1/2)`
C is the point of intersection of the lines x + 2y = 3 and 3x + y = 3.
Solving the above equations, we get
x = `3/5`, y = `6/5`
∴ C ≡ `(3/5, 6/5)`
Here, the objective function is Z = 6x + 21y
∴ Z at A(4, 0) = 6(4) + 21(0) = 24
Z at B`(2, 1/2) = 6(2) + 21(1/2)`
= `12 + 21/2`
= `45/2`
= 22.5
Z at C`(3/5, 6/5) = 6(3/5) + 21(6/5)`
= `18/5 + 126/5`
= `144/5`
= 28.8
Z at D(0, 3) = 6(0) + 21(3) = 63
∴ Z has minimum value 22.5 at B`(2, 1/2)`.
∴ Z has minimum value 22.5 when x = 2 and y = 0.5.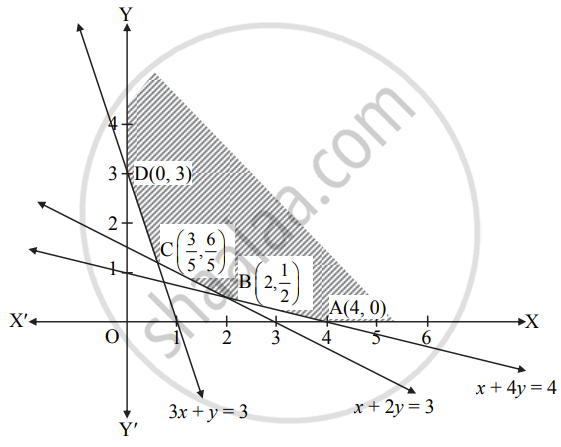
APPEARS IN
संबंधित प्रश्न
Find the feasible solution of the following inequation:
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
A furniture dealer deals in tables and chairs. He has ₹ 1,50,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 1500 and a chair ₹ 750. Construct the inequations and find the feasible solution.
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14. 22 and 1 units of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients:
| Fodder → | Fodder 1 | Fodder 2 |
| Nutrient ↓ | ||
| Nutrients A | 2 | 1 |
| Nutrients B | 2 | 3 |
| Nutrients C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder 2 ₹ 2. Formulate the LPP to minimize the cost.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
A company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the table below:
| Fertilizers→ | F1 | F2 | Availability |
| Raw Material ↓ | |||
| A | 2 | 3 | 40 |
| B | 1 | 4 | 70 |
By selling one unit of F1 and one unit of F2, the company gets a profit of ₹ 500 and ₹ 750 respectively. Formulate the problem as LPP to maximize the profit.
A doctor has prescribed two different units of foods A and B to form a weekly diet for a sick person. The minimum requirements of fats, carbohydrates and proteins are 18, 28, 14 units respectively. One unit of food A has 4 units of fat, 14 units of carbohydrates and 8 units of protein. One unit of food B has 6 units of fat, 12 units of carbohydrates and 8 units of protein. The price of food A is ₹ 4.5 per unit and that of food B is ₹ 3.5 per unit. Form the LPP, so that the sick person’s diet meets the requirements at a minimum cost.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
The point of which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x, ≥ 0, y ≥ 0 is is obtained at ______.
Of all the points of the feasible region, the optimal value of z obtained at the point lies ______.
The corner points of the feasible solution given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0 are ______.
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
Solve the following LPP:
Minimize z = 4x + 2y
Subject to 3x + y ≥ 27, x + y ≥ 21, x + 2y ≥ 30, x ≥ 0, y ≥ 0
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each units of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufactured per month to maximize profit? How much is the maximum profit?
In a cattle breeding firm, it is prescribed that the food ration for one animal must contain 14, 22, and 1 unit of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit weight of these two contains the following amounts of these three nutrients:
| Nutrient\Fodder | Fodder 1 | Fodder2 |
| Nutrient A | 2 | 1 |
| Nutrient B | 2 | 3 |
| Nutrient C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder ₹ 2 per unit. Formulate the L.P.P. to minimize the cost.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B.
| Raw Material \Chemical | A | B | Availability |
| p | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. Formulate the problem as L.P.P. to maximize the profit.
Choose the correct alternative :
Of all the points of the feasible region the optimal value of z is obtained at a point
Choose the correct alternative :
Feasible region; the set of points which satify.
Choose the correct alternative :
The corner points of the feasible region are (0, 0), (2, 0), `(12/7, 3/7)` and (0,1) then the point of maximum z = 7x + y
If the corner points of the feasible region are (0, 0), (3, 0), (2, 1) and `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
The feasible region is the set of point which satisfy.
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Maximize z = −x + 2y subjected to constraints x + y ≥ 5, x ≥ 3, x + 2y ≥ 6, y ≥ 0 is this LPP solvable? Justify your answer.
Choose the correct alternative:
Z = 9x + 13y subjected to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, 0 ≤ x, y was found to be maximum at the point
The constraint that in a particular XII class, number of boys (y) are less than number of girls (x) is given by ______
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
Maximize: z = 3x1 + 4x2 subject to 2x1 + x2 ≤ 40, 2x1 + 5x2 ≤ 180, x1, x2 ≥ 0. In the LPP, which one of the following is feasible comer point?
A solution which maximizes or minimizes the given LPP is called
The maximum value of the objective function Z = 3x + 5y subject to the constraints x ≥ 0, y ≥ 0 and 2x + 5y ≤ 10 is
Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
The maximum value of Z = 9x + 13y subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is ______.
Food F1 contains 2, 6, 1 units and food F2 contains 1, 1, 3 units of proteins, carbohydrates, fats respectively per kg. 8, 12 and 9 units of proteins, carbohydrates and fats is the weekly minimum requirement for a person. The cost of food F1 is Rs. 85 and food F2 is Rs. 40 per kg. Formulate the L.P.P. to minimize the cost.
