Advertisements
Advertisements
Question
Minimize z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
Solution
To draw the feasible region, construct table as follows:
| Inequality | x + 2y ≥ 3 | x + 4y ≥ 4 | 3x + y ≥ 3 |
| Corresponding equation (of line) | x + 2y = 3 | x + 4y = 4 | 3x + y = 3 |
| Intersection of line with X-axis | (3, 0) | (4, 0) | (1, 0) |
| Intersection of line with Y-axis | `(0, 3/2)` | (0, 1) | (0, 3) |
| Region | Non-origin side | Non-origin side | Non-origin side |
x ≥ 0, y ≥ 0 represent 1st quadrant.
Shaded portion XABCDY is the feasible region, whose vertices are A(4, 0), B, C and D(0, 3).
B is the point of intersection of the lines x + 4y = 4 and x + 2y = 3.
Solving the above equations, we get
x = 2, y = `1/2`
∴ B ≡ `(2, 1/2)`
C is the point of intersection of the lines x + 2y = 3 and 3x + y = 3.
Solving the above equations, we get
x = `3/5`, y = `6/5`
∴ C ≡ `(3/5, 6/5)`
Here, the objective function is Z = 6x + 21y
∴ Z at A(4, 0) = 6(4) + 21(0) = 24
Z at B`(2, 1/2) = 6(2) + 21(1/2)`
= `12 + 21/2`
= `45/2`
= 22.5
Z at C`(3/5, 6/5) = 6(3/5) + 21(6/5)`
= `18/5 + 126/5`
= `144/5`
= 28.8
Z at D(0, 3) = 6(0) + 21(3) = 63
∴ Z has minimum value 22.5 at B`(2, 1/2)`.
∴ Z has minimum value 22.5 when x = 2 and y = 0.5.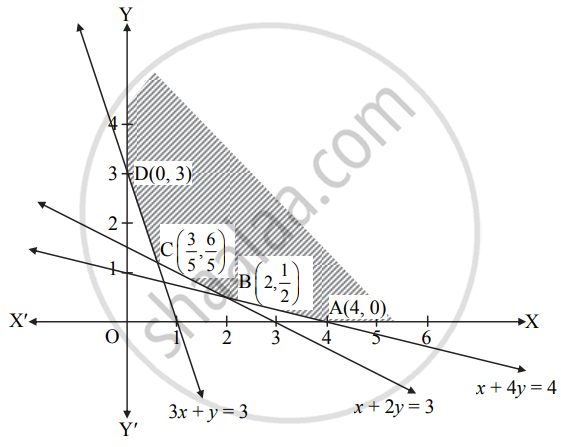
APPEARS IN
RELATED QUESTIONS
Find the feasible solution of the following inequation:
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
Solve the following LPP by graphical method:
Maximize z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Select the appropriate alternatives for each of the following question:
The value of objective function is maximum under linear constraints
The maximum value of z = 5x + 3y subject to the constraints 3x + 5y ≤ 15, 5x + 2y ≤ 10, x, y ≥ 0 is ______.
The maximum value of z = 10x + 6y subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x, ≥ 0, y ≥ 0 is ______.
Of all the points of the feasible region, the optimal value of z obtained at the point lies ______.
If the corner points of the feasible solution are (0, 10), (2, 2) and (4, 0), then the point of minimum z = 3x + 2y is ______.
Solve the following LPP:
Maximize z = 4x1 + 3x2 subject to
3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0.
A company produces mixers and food processors. Profit on selling one mixer and one food processor is Rs 2,000 and Rs 3,000 respectively. Both the products are processed through three machines A, B, C. The time required in hours for each product and total time available in hours per week on each machine arc as follows:
| Machine | Mixer | Food Processor | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced in order to maximize the profit?
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B.
| Raw Material \Chemical | A | B | Availability |
| p | 3 | 2 | 120 |
| Q | 2 | 5 | 160 |
The company gets profits of ₹ 350 and ₹ 400 by selling one unit of A and one unit of B respectively. Formulate the problem as L.P.P. to maximize the profit.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. If maximum availability of Machine M1 is 10 hours and that of Machine M2 is 12 hours, then formulate the L.P.P. to maximize the profit.
A company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the table below:
| Raw Material\Fertilizers | F1 | F2 | Availability |
| A | 2 | 3 | 40 |
| B | 1 | 4 | 70 |
By selling one unit of F1 and one unit of F2, company gets a profit of ₹ 500 and ₹ 750 respectively. Formulate the problem as L.P.P. to maximize the profit.
Choose the correct alternative :
Of all the points of the feasible region the optimal value of z is obtained at a point
Choose the correct alternative :
Solution of LPP to minimize z = 2x + 3y st. x ≥ 0, y ≥ 0, 1≤ x + 2y ≤ 10 is
Choose the correct alternative :
The corner points of the feasible region are (0, 0), (2, 0), `(12/7, 3/7)` and (0,1) then the point of maximum z = 7x + y
Fill in the blank :
A dish washing machine holds up to 40 pieces of large crockery (x) This constraint is given by_______.
The feasible region is the set of point which satisfy.
The point of which the maximum value of z = x + y subject to constraints x + 2y ≤ 70, 2x + y ≤ 90, x ≥ 0, y ≥ 0 is obtained at
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Minimize z = 2x + 4y is subjected to 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
Choose the correct alternative:
Z = 9x + 13y subjected to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, 0 ≤ x, y was found to be maximum at the point
The variables involved in LPP are called ______
Solve the following linear programming problems by graphical method.
Minimize Z = 3x1 + 2x2 subject to the constraints 5x1 + x2 ≥ 10; x1 + x2 ≥ 6; x1 + 4x2 ≥ 12 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
Maximize: z = 3x1 + 4x2 subject to 2x1 + x2 ≤ 40, 2x1 + 5x2 ≤ 180, x1, x2 ≥ 0. In the LPP, which one of the following is feasible comer point?
A solution which maximizes or minimizes the given LPP is called
In the given graph the coordinates of M1 are

A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
The LPP to maximize Z = x + y, subject to x + y ≤ 1, 2x + 2y ≥ 6, x ≥ 0, y ≥ 0 has ________.
The minimum value of z = 5x + 13y subject to constraints 2x + 3y ≤ 18, x + y ≥ 10, x ≥ 0, y ≥ 2 is ______
The point which provides the solution of the linear programming problem, Max.(45x + 55y) subject to constraints x, y ≥ 0, 6x + 4y ≤ 120, 3x + 10y ≤ 180, is ______
Solve the following LP.P.
Maximize z = 13x + 9y,
Subject to 3x + 2y ≤ 12,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.
The optimal value of the objective function is attained at the ______ of feasible region.
Shamli wants to invest ₹ 50, 000 in saving certificates and PPF. She wants to invest atleast ₹ 15,000 in saving certificates and at least ₹ 20,000 in PPF. The rate of interest on saving certificates is 8% p.a. and that on PPF is 9% p.a. Formulation of the above problem as LPP to determine maximum yearly income, is ______.
The maximum value of Z = 9x + 13y subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is ______.
Food F1 contains 2, 6, 1 units and food F2 contains 1, 1, 3 units of proteins, carbohydrates, fats respectively per kg. 8, 12 and 9 units of proteins, carbohydrates and fats is the weekly minimum requirement for a person. The cost of food F1 is Rs. 85 and food F2 is Rs. 40 per kg. Formulate the L.P.P. to minimize the cost.
Sketch the graph of the following inequation in XOY co-ordinate system.
x + y ≤ 0
