Advertisements
Advertisements
प्रश्न
Solution which satisfy all constraints is called ______ solution.
उत्तर
Solution which satisfy all constraints is called feasible solution.
APPEARS IN
संबंधित प्रश्न
Find the feasible solution of the following inequation:
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Find the feasible solution of the following inequations:
x - 2y ≤ 2, x + y ≥ 3, - 2x + y ≤ 4, x ≥ 0, y ≥ 0
A furniture dealer deals in tables and chairs. He has ₹ 1,50,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 1500 and a chair ₹ 750. Construct the inequations and find the feasible solution.
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14. 22 and 1 units of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients:
| Fodder → | Fodder 1 | Fodder 2 |
| Nutrient ↓ | ||
| Nutrients A | 2 | 1 |
| Nutrients B | 2 | 3 |
| Nutrients C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder 2 ₹ 2. Formulate the LPP to minimize the cost.
Solve the following LPP by graphical method:
Maximize z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Minimize z = 6x + 2y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
The point of which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x, ≥ 0, y ≥ 0 is is obtained at ______.
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
Solve the following LPP:
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0.
Find graphical solution for the following system of linear in equation:
3x + 4y ≤ 12, x - 2y ≥ 2, y ≥ - 1
Solve the following LPP:
Minimize z = 4x + 2y
Subject to 3x + y ≥ 27, x + y ≥ 21, x + 2y ≥ 30, x ≥ 0, y ≥ 0
A carpenter makes chairs and tables. Profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines: Assembling, Finishing and Polishing. The time required for each product in hours and availability of each machine is given by the following table:
| Product → | Chair (x) | Table (y) | Available time (hours) |
| Machine ↓ | |||
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate the above problem as LPP. Solve it graphically
Solve the following L.P.P. by graphical method:
Maximize: Z = 4x + 6y
Subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Choose the correct alternative :
Of all the points of the feasible region the optimal value of z is obtained at a point
Choose the correct alternative :
The corner points of the feasible region are (0, 0), (2, 0), `(12/7, 3/7)` and (0,1) then the point of maximum z = 7x + y
Choose the correct alternative :
The half plane represented by 3x + 2y ≤ 0 constraints the point.
Minimize z = 7x + y subjected to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Maximize z = −x + 2y subjected to constraints x + y ≥ 5, x ≥ 3, x + 2y ≥ 6, y ≥ 0 is this LPP solvable? Justify your answer.
Choose the correct alternative:
Z = 9x + 13y subjected to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, 0 ≤ x, y was found to be maximum at the point
Constraints are always in the form of ______ or ______.
Solve the following linear programming problems by graphical method.
Minimize Z = 3x1 + 2x2 subject to the constraints 5x1 + x2 ≥ 10; x1 + x2 ≥ 6; x1 + 4x2 ≥ 12 and x1, x2 ≥ 0.
The maximum value of Z = 3x + 5y, subject to 3x + 2y ≤ 18, x ≤ a, y ≤ 6, x, y ≥ 0 is ______.
The point which provides the solution of the linear programming problem, Max.(45x + 55y) subject to constraints x, y ≥ 0, 6x + 4y ≤ 120, 3x + 10y ≤ 180, is ______
Solve the following LP.P.
Maximize z = 13x + 9y,
Subject to 3x + 2y ≤ 12,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.
The optimal value of the objective function is attained at the ______ of feasible region.
The maximum value of Z = 9x + 13y subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is ______.
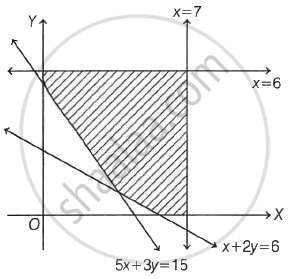
For the following shaded region, the linear constraint are:
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
Two kinds of foods A and B are being considered to form a weekly diet. The minimum weekly requirements of fats, Carbohydrates and proteins are 12, 16 and 15 units respectively. One kg of food A has 2, 8 and 5 units respectively of these ingredients and one kg of food B has 6, 2 and 3 units respectively. The price of food A is Rs. 4 per kg and that of food B is Rs. 3 per kg. Formulate the L.P.P. and find the minimum cost.
Food F1 contains 2, 6, 1 units and food F2 contains 1, 1, 3 units of proteins, carbohydrates, fats respectively per kg. 8, 12 and 9 units of proteins, carbohydrates and fats is the weekly minimum requirement for a person. The cost of food F1 is Rs. 85 and food F2 is Rs. 40 per kg. Formulate the L.P.P. to minimize the cost.
