Advertisements
Advertisements
प्रश्न
Find the feasible solution of the following inequations:
x - 2y ≤ 2, x + y ≥ 3, - 2x + y ≤ 4, x ≥ 0, y ≥ 0
उत्तर
First we draw the lines AB, CD and EF whose equations are x - 2y = 2, x + y = 3 and - 2x + y = 4 respectively.
| Line | Equation | Points on the X-axis | Points on the Y-axis | Sign | Region |
| AB | x - 2y = 2 | A(2, 0) | B(0,-1) | ≤ | origin side of line AB |
| CD | x + y = 3 | C(3, 0) | D(0,3) | ≥ | non-origin side of line AB |
| EF | - 2x + y = 4 | E(-2,0) | F(0,4) | ≤ | origin side of line EF |
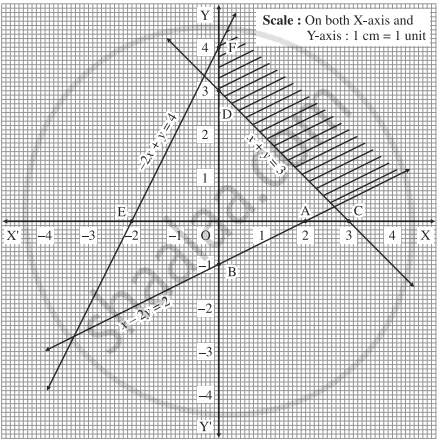
The feasible solution is shaded in the graph.
APPEARS IN
संबंधित प्रश्न
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14. 22 and 1 units of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients:
| Fodder → | Fodder 1 | Fodder 2 |
| Nutrient ↓ | ||
| Nutrients A | 2 | 1 |
| Nutrients B | 2 | 3 |
| Nutrients C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder 2 ₹ 2. Formulate the LPP to minimize the cost.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
If John drives a car at a speed of 60 km/hour, he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 km/hour, the cost of petrol increases ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
Solve the following LPP by graphical method:
Maximize z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Solve the following LPP by graphical method:
Minimize z = 8x + 10y, subject to 2x + y ≥ 7, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0.
Of all the points of the feasible region, the optimal value of z obtained at the point lies ______.
The corner points of the feasible solution given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0 are ______.
The half-plane represented by 3x + 2y < 8 contains the point ______.
Solve each of the following inequations graphically using XY-plane:
4x - 18 ≥ 0
Solve each of the following inequations graphically using XY-plane:
y ≤ - 3.5
Sketch the graph of the following inequation in XOY co-ordinate system:
|x + 5| ≤ y
Solve the following LPP:
Maximize z = 4x1 + 3x2 subject to
3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0.
Solve the following LPP:
Maximize z =60x + 50y subject to
x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0.
In a cattle breeding firm, it is prescribed that the food ration for one animal must contain 14, 22, and 1 unit of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit weight of these two contains the following amounts of these three nutrients:
| Nutrient\Fodder | Fodder 1 | Fodder2 |
| Nutrient A | 2 | 1 |
| Nutrient B | 2 | 3 |
| Nutrient C | 1 | 1 |
The cost of fodder 1 is ₹ 3 per unit and that of fodder ₹ 2 per unit. Formulate the L.P.P. to minimize the cost.
Solve the following L.P.P. by graphical method:
Maximize: Z = 4x + 6y
Subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Choose the correct alternative :
Solution of LPP to minimize z = 2x + 3y st. x ≥ 0, y ≥ 0, 1≤ x + 2y ≤ 10 is
Choose the correct alternative :
The corner points of the feasible region given by the inequations x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0, are
If the corner points of the feasible region are (0, 0), (3, 0), (2, 1) and `(0, 7/3)` the maximum value of z = 4x + 5y is ______.
Choose the correct alternative :
The half plane represented by 3x + 2y ≤ 0 constraints the point.
Fill in the blank :
The optimal value of the objective function is attained at the _______ points of feasible region.
State whether the following is True or False :
Saina wants to invest at most ₹ 24000 in bonds and fixed deposits. Mathematically this constraints is written as x + y ≤ 24000 where x is investment in bond and y is in fixed deposits.
State whether the following is True or False :
The point (1, 2) is not a vertex of the feasible region bounded by 2x + 3y ≤ 6, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
The point of which the maximum value of z = x + y subject to constraints x + 2y ≤ 70, 2x + y ≤ 90, x ≥ 0, y ≥ 0 is obtained at
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Maximize z = 5x + 2y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Minimize z = 2x + 4y is subjected to 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
Choose the correct alternative:
Z = 9x + 13y subjected to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, 0 ≤ x, y was found to be maximum at the point
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
The minimum value of the objective function Z = x + 3y subject to the constraints 2x + y ≤ 20, x + 2y ≤ 20, x > 0 and y > 0 is
A firm manufactures pills in two sizes A and B. Size A contains 2 mgs of aspirin, 5 mgs of bicarbonate and 1 mg of codeine. Size B contains 1 mg. of aspirin, 8 mgs. of bicarbonate and 6 mgs. of codeine. It is found by users that it requires at least 12 mgs. of aspirin, 74 mgs. of bicarbonate and 24 mgs. of codeine for providing immediate relief. It is required to determine the least number of pills a patient should take to get immediate relief. Formulate the problem as a standard LLP.
The maximum value of Z = 3x + 5y, subject to 3x + 2y ≤ 18, x ≤ a, y ≤ 6, x, y ≥ 0 is ______.
Solution which satisfy all constraints is called ______ solution.
The maximum value of Z = 9x + 13y subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is ______.
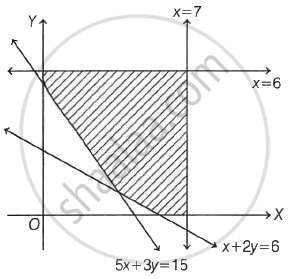
For the following shaded region, the linear constraint are:
Solve the following problems by graphical method:
Maximize z = 4x + 2y subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0 y ≥ 0
Solve the following LPP:
Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
