Advertisements
Advertisements
प्रश्न
Solve the following quadratic equation by factorization method
`sqrt("a"("a" - 7)) = 3sqrt(2)`
उत्तर
`sqrt("a"("a" - 7)) = 3sqrt(2)`
Squaring on both sides
a(a – 7) = `(3sqrt(2))^2`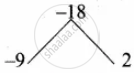
a2 – 7a = 18
a2 – 7a – 18 = 0
(a – 9) (a + 2) = 0
a – 9 = 0 or a + 2 = 0
The roots are – 2 and 9
APPEARS IN
संबंधित प्रश्न
Find the sum and product of the roots for the following quadratic equation
x2 + 3x = 0
Solve the following quadratic equation by factorization method
`sqrt(2)x^2 + 7x + 5sqrt(2)` = 0
Determine the nature of the roots for the following quadratic equation
x2 – x – 1 = 0
If the roots of the equation (c2 – ab)x2 – 2(a2 – bc)x + b2 – ac = 0 are real and equal prove that either a = 0 (or) a3 + b3 + c3 = 3abc
Write the following expression in terms of α + β and αβ
`alpha/(3beta) + beta/(3alpha)`
Write the following expression in terms of α + β and αβ
`1/(alpha^2beta) + 1/(beta^2alpha)`
The roots of the equation x2 + 6x – 4 = 0 are α, β. Find the quadratic equation whose roots are `2/alpha` and `2/beta`
The roots of the equation x2 + 6x – 4 = 0 are α, β. Find the quadratic equation whose roots are α2β and β2α
If one root of the equation 3x2 + kx + 81 = 0 (having real roots) is the square of the other then find k
`x/(x^2 - 25) - 8/(x^2 + 6x + 5)` gives
