Advertisements
Advertisements
प्रश्न
Solve the inequation:
`– 1 < 3 – "x"/5 ≤ 1`
उत्तर
`– 1 < 3 – "x"/5 ≤ 1`
Multiplying the inequation by 5, the sign of inequality changes
5 > – 15 + x > – 5
Adding 15 on both the sides, we get
20 > x > 10
⇒ 10 < x < 20
The solution contains all the real values of x lying between 10 and 20, excluding the boundary value.
The solution set can be written in the form of open interval (10, 20).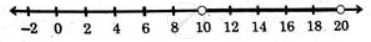
APPEARS IN
संबंधित प्रश्न
Solve the following inequation: 3x – 36 > 0
Solve the following inequation:
7x – 25 ≤ – 4
Solve the following inequation: `0 < ("x" - 5)/4 < 3`
Solve the following inequation: |7x – 4| < 10
Solve the inequation:
3x + 1 ≥ 6x – 4
Solve the inequation:
`3/4 "x" - 6 ≤ "x" - 7`
Solve the inequation:
2|4 – 5x| ≥ 9
Solve the inequation:
|2x + 7| ≤ 25
Solve the inequation:
`("x" + 5)/("x" - 3) < 0`
To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94, and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
The region represented by {z = x + iy ∈ C : |z| – Re(z) ≤ 1} is also given by the inequality is ______.
Consider the two sets : A = {m ∈ R : both the roots of x2 – (m + 1)x + m + 4 = 0 are real} and B = [–3, 5). Which of the following is not true?
Let S be the set of all real roots of the equation, 3x(3x – 1) + 2 = |3x – 1| + |3x – 2|. Then S ______.
Let Z be the set of integers. lf A = `{x ∈ Z: 2^((x + 2)(x^2 – 5x + 6)) = 1}` and B = {x ∈ Z: –3 < 2x – 1 < 9}, then the number of subsets of the set A × B, is ______.
All the-pairs (x, y) that satisfy the inequality `2^sqrt(sin^2x - 2sinx + 5), 1/(4^(sin^2y)) ≤ 1` also satisfy the equation ______.
