Advertisements
Advertisements
प्रश्न
State and explain the theorem of parallel axes.
उत्तर
Statement: The moment of inertia (Io) of an object about any axis is the sum of its moment of inertia (Ic) about an axis parallel to the given axis, and passing through the centre of mass and the product of the mass of the object and the square of the distance between the two axes. Mathematically, Io = Ic + Mh2
Proof:
- Consider an object of mass M. Axis MOP is an axis passing through point O.
- Axis ACB is passing through the centre of mass C of the object, parallel to the axis MOP, and at a distance h from it (∴ h = CO).

The theorem of parallel axes - Consider a mass element ‘dm’ located at point D. Perpendicular on OC (produced) from point D is DN.
- The moment of inertia of the object about the axis ACB is Ic = ∫ (DC)2 dm, and about the axis MOP, it is Io = ∫ (DO)2 dm.
- Io = ∫ (DO)2 dm
= ∫ [(DN)2 + (NO)2] dm
= ∫ [(DN)2 + (NC)2 + 2 . NC . CO + (CO)2]dm
= ∫ [(DC)2 + 2NC . h + h2]dm ...........….(using Pythagoras theorem in ∆DNC)
= ∫ (DC)2 dm + 2h ∫ NC . dm + h2 ∫ dm
Now, ∫ (DC)2 dm = Ic and ∫ dm = M - NC is the distance of a point from the centre of mass. Any mass distribution is symmetric about the centre of mass. Thus, from the definition of the centre of mass, ∫ NC . dm = 0
∴ Io = Ic + M.h2
This is the mathematical form of the theorem of parallel axes.
APPEARS IN
संबंधित प्रश्न
State the theorem of perpendicular axes about moment of inertia.
State an expression for the moment of intertia of a solid uniform disc, rotating about an axis passing through its centre, perpendicular to its plane. Hence derive an expression for the moment of inertia and radius of gyration:
i. about a tangent in the plane of the disc, and
ii. about a tangent perpendicular to the plane of the disc.
Prove the theorem of parallel axes about moment of inertia
State Brewster's law.
Prove the theorem of perpendicular axes.
(Hint: Square of the distance of a point (x, y) in the x–y plane from an axis through the origin perpendicular to the plane is x2 + y2).
Prove the theorem of parallel axes.
(Hint: If the centre of mass is chosen to be the origin `summ_ir_i = 0`
Find the radius of gyration of circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of its particles.
Answer in brief:
State the conditions under which the theorems of parallel axes and perpendicular axes are applicable. State the respective mathematical expressions.
A string of length ℓ fixed at one end carries a mass m at the other. The string makes 2/π revolutions/sec around the vertical axis through the fixed end. The tension in the string is ______.
A solid cylinder of radius r and mass M rolls down an inclined plane of height h. When it reaches the bottom of the plane, then its rotational kinetic energy is ____________.
(g = acceleration due to gravity)
When a 12000 joule of work is done on a flywheel, its frequency of rotation increases from 10 Hz to 20 Hz. The moment of inertia of flywheel about its axis of rotation is ______. (π2 = 10)
A circular disc 'X' of radius 'R' made from iron plate of thickness 't' has moment of inertia 'Ix' about an axis passing through the centre of disc and perpendicular to its plane. Another disc 'Y' of radius '3R' made from an iron plate of thickness `("t"/3)` has moment of inertia 'Iy' about the s same as that of disc X. The relation between Ix and ly is ______.
Two bodies have their moments of inertia I and 2I respectively about their axes of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio ______.
A wheel of moment of inertia 2 kg m2 is rotating at a speed of 25 rad/s. Due to friction on the axis, it comes to rest in 10 minutes. Total work done by friction is ______.
The moment of inertia of a uniform square plate about an axis perpendicular to its plane and passing through the centre is `"Ma"^2/6` where M is the mass and 'a' is the side of square plate. Moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corner is ______.
A solid sphere of mass 'M' and radius 'R' is rotating about its diameter. A disc of same mass and radius is also rotating about an axis passing through its centre and perpendicular to the plane but angular speed is twice that of the sphere. The ratio of kinetic energy of disc to that of sphere is ______.
From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
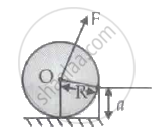
A uniform cylinder of mass M and radius R is to be pulled over a step of height a (a < R) by applying a force F at its centre 'O' perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of F required is:
Two particles A and B having equal charges are placed at a distance d apart. A third charged particle placed on the perpendicular bisection of AB at distance x. The third particle experiences maximum force when ______.
A metal ring has a moment of inertia 2 kg·m2 about a transverse axis through its centre. It is melted and recast into a thin uniform disc of the same radius. What will be the disc's moment of inertia about its diameter?
A uniform disc of mass 10 kg and radius 60 cm rotates about an axis perpendicular to its plane and passing through its centre at 1200 rpm. Calculate its rotation kinetic energy. [Take π2 = 10]
State and prove the theorem of the parallel axis about the moment of inertia.
Prove the theorem of perpendicular axes about the moment of inertia.
