Advertisements
Advertisements
प्रश्न
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx(bar"b" xx bar"c")`
उत्तर
This is vector product of two vectors. Therefore, this expression is meaningful and it is a vector.
APPEARS IN
संबंधित प्रश्न
If `veca=xhati+2hatj-zhatk and vecb=3hati-yhatj+hatk` are two equal vectors ,then write the value of x+y+z
For what value of 'a' the vectors \[2 \hat{i} - 3 \hat{j} + 4 \hat{k} \text{ and }a \hat{i} + 6 \hat{j} - 8 \hat{k}\] are collinear?
If \[\vec{a} , \vec{b}\] are the vectors forming consecutive sides of a regular hexagon ABCDEF, then the vector representing side CD is
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
ABCD is a parallelogram with AC and BD as diagonals.
Then, \[\overrightarrow{AC} - \overrightarrow{BD} =\]
Find the components along the coordinate axes of the position vector of the following point :
P(3, 2)
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
If `veca` and `vecb` are non- collinear vectors, find the value of x such that the vectors `barα = (x - 2)veca + vecb` and `barβ = (3+2x)bara - 2barb` are collinear.
If` vec"a" = 2hat"i" + 3hat"j" + + hat"k", vec"b" = hat"i" - 2hat"j" + hat"k" "and" vec"c" = -3hat"i" + hat"j" + 2hat"k", "find" [vec"a" vec"b" vec"c"]`
OABCDE is a regular hexagon. The points A and B have position vectors `bar"a"` and `bar"b"` respectively referred to the origin O. Find, in terms of `bar"a"` and `bar"b"` the position vectors of C, D and E.
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
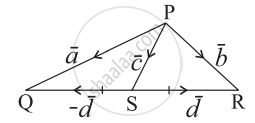
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
If the sum of two unit vectors is itself a unit vector, then the magnitude of their difference is ______.
If two sides of a triangle are `hat"i" + 2hat"j" and hat"i" + hat"k"`, find the length of the third side.
Find the unit vectors that are parallel to the tangent line to the parabola y = x2 at the point (2, 4).
A point P with position vector `(- 14hat"i" + 39hat"j" + 28hat"k")/5` divides the line joining A (1, 6, 5) and B in the ratio 3 : 2, then find the point B.
Express `hat"i" + 4hat"j" - 4hat"k"` as the linear combination of the vectors `2hat"i" - hat"j" + 3hat"k", hat"i" - 2hat"j" + 4hat"k"` and `- hat"i" + 3hat"j" - 5hat"k"`.
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0) and (0, 0, c). What is the area of the triangle with these vertices?
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" xx bar"c")`
The vector eqliation of line 2x - 2 = 3y + 1 = 6z - 2 is
a and b are non-collinear vectors. If p = (2x + 1) a - band q = (x - 2)a +b are collinear vectors, then x = ______.
lf `overlinea` and `overlineb` be two unit vectors and θ is the angle between them, then `|overlinea - overlineb|` is equal to ______
If `vec"a" = 2hat"i" - hat"j" + hat"k", vec"b" = hat"i" + hat"j" - 2hat"k"` and `vec"c" = hat"i" + 3hat"j" - hat"k"`, find `lambda` such that `vec"a"` is perpendicular to `lambdavec"b" + vec"c"`.
The area of the parallelogram whose adjacent sides are `hat"i" + hat"k"` and `2hat"i" + hat"j" + hat"k"` is ______.
If `veca` and `vecb` are unit vectors, then what is the angle between `veca` and `vecb` for `sqrt(3) veca - vecb` to be a unit vector?
If `vec"a", vec"b", vec"c"` determine the vertices of a triangle, show that `1/2[vec"b" xx vec"c" + vec"c" xx vec"a" + vec"a" xx vec"b"]` gives the vector area of the triangle. Hence deduce the condition that the three points `vec"a", vec"b", vec"c"` are collinear. Also find the unit vector normal to the plane of the triangle.
Classify the following measures as scalar and vector.
2 meters north-west
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
`bara, barb` and `barc` are three vectors such that `veca + vecb + vecc` 20, `|bara| = 1, |barb| = 2` and `|barc| = 3`. Then `bara. barb + barb.barc + bar(c.a)` is equal to
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
Find `|veca xx vecb|`, if `veca = hati - 7hatj + 7hatk` and `vecb = 3hati - 2hatj + 2hatk`
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
The angles of a triangle, two of whose sides are represented by the vectors `sqrt(3)(veca xx vecb)` and `vecb - (veca.vecb)veca` where `vecb` is a non-zero vector and `veca` is a unit vector are ______.
In the triangle PQR, `bar("P""Q")`= `2 bar"a"` and `bar ("QR")` = `2 barb`.The mid - point of PR is M. Find following vector in term of `bar a ` and `barb.`
- `bar("P""R")`
- `bar("P""M")`
- `bar("Q""M")`
Check whether the vectors `2hati + 2hatj + 3hat k, -3hati + 3hatj + 2hat k` and `3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
