Advertisements
Advertisements
प्रश्न
Suppose that the electric field amplitude of an electromagnetic wave is E0 = 120 N/C and that its frequency is v = 50.0 MHz.
- Determine B0, ω, k, and λ.
- Find expressions for E and B.
उत्तर
Electric field amplitude, E0 = 120 N/C
Frequency of source, v = 50.0 MHz = 50 × 106 Hz
Speed of light, c = 3 × 108 m/s
(a) Magnitude of magnetic field strength is given as:
`"B"_0 = "E"_0/"c"`
= `120/(3 xx 10^8)`
= 4 × 10−7 T
= 400 nT
Angular frequency of the source is given as:
ω = 2πv
= 2π × 50 × 106
= 3.14 × 108 rad/s
Propagation constant is given as:
`"k" = ω/"c"`
= `(3.14 xx 10^8)/(3 xx 10^8)`
= 1.05 rad/m
Wavelength of the wave is given as:
`lambda = "c"/"v"`
= `(3 xx 10^8)/(50 xx 10^6)`
= 6.0 m
(b) Suppose the wave is propagating in the positive x-direction. Then, the electric field vector will be in the positive y-direction and the magnetic field vector will be in the positive z-direction. This is because all three vectors are mutually perpendicular.
Equation of the electric field vector is given as:
`vec("E") = "E"_0 sin ("k""x" - ω"t")hat"j"`
= `120 sin [1.05"x" - 3.14 xx 10^8"t"]hat"j"`
Magnetic field vector is given as:
`vec("B") = "B"_0 sin ("kx" - ω"t")hat"k"`
`vec("B") = (4 xx 10^-7) sin [1.05"x" - 3.14 xx 10^8"t"]hat"k"`
APPEARS IN
संबंधित प्रश्न
In a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0 × 1010 Hz and amplitude 48 V m−1.
- What is the wavelength of the wave?
- What is the amplitude of the oscillating magnetic field?
- Show that the average energy density of the E field equals the average energy density of the B field.
[c = 3 × 108 m s−1]
Draw a sketch of linearly polarized em waves propagating in the Z-direction. Indicate the directions of the oscillating electric and magnetic fields.
Arrange the following electromagnetic waves in order of increasing frequency:
ϒ-rays, microwaves, infrared rays and ultraviolet rays.
How are the magnitudes of the electric and magnetic fields related to velocity of the em wave?
Can an electromagnetic wave be polarised?
An electromagnetic wave going through vacuum is described by
E = E0 sin (kx − ωt); B = B0 sin (kx − ωt).
Which of the following equations is true?
The energy contained in a small volume through which an electromagnetic wave is passing oscillates with
This is an example of step-up transformer.
The dimension of `1/(mu_0 ∈_0)` is
An e.m. wave is propagating in a medium with a velocity `vec"v" = "v" hat"i"`. The instantaneous oscillating electric field of this e.m. wave is along +y-axis, then the direction of an oscillating magnetic field of the e.m. wave will be along:
What are electromagnetic waves?
Write a short note on the X-ray.
A pulse of light of duration 10-6 s is absorbed completely by a small object initially at rest. If the power of the pulse is 60 x 10-3 W, calculate the final momentum of the object.
Maxwell's equation describe the fundamental law of
For which frequency of light, the eye is most sensitive?
Poynting vectors S is defined as a vector whose magnitude is equal to the wave intensity and whose direction is along the direction of wave propagation. Mathematically, it is given by `S = 1/mu_0 E xx B`. Show the nature of S vs t graph.
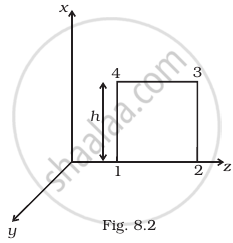
A plane EM wave travelling in vacuum along z direction is given by `E = E_0 sin(kz - ωt)hati` and `B = B_0 sin(kz - ωt)hatj`
- Evaluate `oint E.dl` over the rectangular loop 1234 shown in figure.
- Evaluate `int B.ds` over the surface bounded by loop 1234.
- Use equation `oint E.dl = (-dphi_B)/(dt)` to prove `E_0/B_0` = c.
- By using similar process and the equation `ointB.dl = mu_0I + ε_0 (dphi_E)/(dt)`, prove that c = `1/sqrt(mu_0ε_0)`
A plane EM wave travelling along z direction is described by `E = E_0 sin (kz - ωt)hati` and `B = B_0 sin (kz - ωt)hatj`. show that
- The average energy density of the wave is given by `u_(av) = 1/4 ε_0E_0^2 + 1/4 B_0^2/mu_0`.
- The time averaged intensity of the wave is given by `I_(av) = 1/2 cε_0 E_0^2`.
Which of the following statement is NOT true about the properties of electromagnetic waves?
Name the electromagnetic wave/radiation which is used to study crystal structure.
