Advertisements
Advertisements
प्रश्न
The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically.
उत्तर
Let cost of one bat = Rs x
Cost of one ball = Rs y
3 bats and 6 balls for Rs 3900 So that
3x + 6y = 3900
Dividing equation by 3, we get
x + 3y = 1300
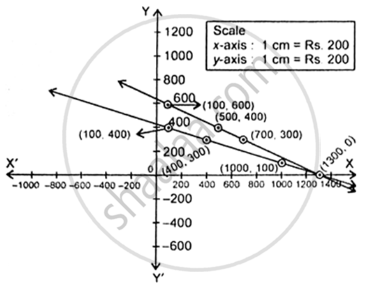
Graphical representation:
we have,
3x + 6y = 3900
3(x + 2y) = 3900
x + 2y = 1300
a = 1300 - 2y
Thus, we have following table:
| x | 1300 | 500 | 700 | 100 |
| y | 0 | 400 | 300 | 600 |
we have, x + 3y = 1300
x = 1300 - 3y
Thus, we have following table:
| x | 1300 | 100 | 400 | 1000 |
| y | 0 | 400 | 300 | 100 |
when we plot the graph of equations, we find that both the lines intersect at the point (1300, 0).
Therefore, a = 1300, y = 0 is the solution of the given system of equations.
संबंधित प्रश्न
If (9/2, 6) is lies on graph of 4x + ky = 12 then find value of k
Find five equations of lines which passes through (3, –5).
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300. Represent the situation algebraically and geometrically.
In the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it:
kx + 2y - 5 = 0
3x + y - 1 = 0
Find the value of k for which each of the following system of equations has infinitely many solutions :
8x + 5y = 9
kx + 10y = 18
Find the value of k for which each of the following system of equations have no solution :
3x - 4y + 7 = 0
kx + 3y - 5 = 0
Find the values of k for which the system
2x + ky = 1
3x – 5y = 7
will have (i) a unique solution, and (ii) no solution. Is there a value of k for which the
system has infinitely many solutions?
Solve for x and y:
9x - 2y = 108, 3x + 7y = 105
Solve for x and y:
`x/3 + y/4 = 11, (5x)/6 - y/3 + 7 = 0`
Solve for x and y:
4x - 3y = 8, 6x - y = `29/3`
Solve for x and y:
2x - `(3y)/4 = 3 ,5x = 2y + 7`
Solve for x and y:
0.4x + 0.3y = 1.7, 0.7x – 0.2y = 0.8.
Solve for x and y:
6x + 5y = 7x + 3y + 1 = 2(x + 6y – 1)
Solve for x and y:
`9/x - 4/y = 8, (13)/x + 7/y = 101`
Solve for x and y:
`5/(x+1) + 2/(y−1) = 1/2, 10/(x+1) - 2/(y−1) = 5/2, where x ≠ 1, y ≠ 1.`
Solve for x and y:
217x + 131y = 913, 131x + 217y = 827
Solve for x and y:
`x + y = a + b, a x – by = a^2 – b^2`
Solve for x and y:
`x + y = a + b, ax - by = a^2 - b^2`
Find the value of k for which the system of equations
kx + 3y = 3, 12x + ky = 6 has no solution.
5 chairs and 4 tables together cost ₹5600, while 4 chairs and 3 tables together cost
₹ 4340. Find the cost of each chair and that of each table
If 45 is subtracted from twice the greater of two numbers, it results in the other number. If 21 is subtracted from twice the smaller number, it results in the greater number. Find the numbers
The denominator of a fraction is greater than its numerator by 11. If 8 is added to both its numerator and denominator, it becomes `3/4`. Find the fraction.
Taxi charges in a city consist of fixed charges per day and the remaining depending upon the distance travelled in kilometers. If a person travels 80km, he pays Rs. 1330, and for travelling 90km, he pays Rs. 1490. Find the fixed charges per day and the rate per km.
The length of a room exceeds its breadth by 3 meters. If the length is increased by 3 meters and the breadth is decreased by 2 meters, the area remains the same. Find the length and the breadth of the room.
Solve the following for x:
`1/(2a+b+2x)=1/(2a)+1/b+1/(2x)`
Find the value(s) of p in (i) to (iv) and p and q in (v) for the following pair of equations:
– 3x + 5y = 7 and 2px – 3y = 1,
if the lines represented by these equations are intersecting at a unique point.
If x = a, y = b is the solution of the equations x – y = 2 and x + y = 4, then the values of a and b are, respectively ______.
A lending library has a fixed charge for first three days and an additional charge for each day thereafter. Rittik paid 27 for a book kept for 7 days and Manmohan paid ₹ 21 for a book kept for 5 days. Find the fixed charges and the charge for each extra day.
