Advertisements
Advertisements
प्रश्न
The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically.
उत्तर
Let cost of one bat = Rs x
Cost of one ball = Rs y
3 bats and 6 balls for Rs 3900 So that
3x + 6y = 3900
Dividing equation by 3, we get
x + 3y = 1300
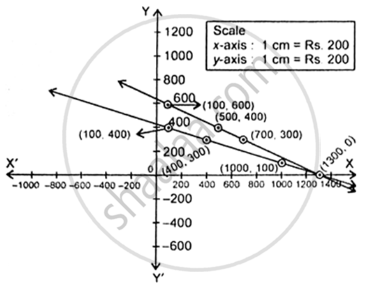
Graphical representation:
we have,
3x + 6y = 3900
3(x + 2y) = 3900
x + 2y = 1300
a = 1300 - 2y
Thus, we have following table:
| x | 1300 | 500 | 700 | 100 |
| y | 0 | 400 | 300 | 600 |
we have, x + 3y = 1300
x = 1300 - 3y
Thus, we have following table:
| x | 1300 | 100 | 400 | 1000 |
| y | 0 | 400 | 300 | 100 |
when we plot the graph of equations, we find that both the lines intersect at the point (1300, 0).
Therefore, a = 1300, y = 0 is the solution of the given system of equations.
संबंधित प्रश्न
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically
Find the value of k for which each of the following system of equations have no solution :
2x - ky + 3 = 0
3x + 2y - 1 = 0
Find the value of k for which the following system of equations has a unique solution:
kx + 3y = 3
12x + ky = 6
Find the value of k for which the system
kx + 2y = 5
3x + y = 1
has (i) a unique solution, and (ii) no solution.
Find the values of a and b for which the following system of equations has infinitely many solutions:
2x + 3y = 7
(a - 1)x + (a + 2)y = 3a
Solve for x and y:
`x/3 + y/4 = 11, (5x)/6 - y/3 + 7 = 0`
Solve for x and y:
`5/x + 6y = 13, 3/x + 4y = 7`
Solve for x and y:
`x + 6/y = 6, 3x - 8/y = 5`
Solve for x and y:
`2x - 3/y = 9, 3x + 7/y = 2`
Solve for x and y:
x + y = 5xy, 3x + 2y = 13xy
Solve for x and y:
`5/(x+1) + 2/(y−1) = 1/2, 10/(x+1) - 2/(y−1) = 5/2, where x ≠ 1, y ≠ 1.`
Solve for x and y:
`x + y = a + b, a x – by = a^2 – b^2`
Find the value of k for which the system of equations has a unique solution:
2x + 3y = 5,
kx - 6y = 8
Show that the system of equations
6x + 5y = 11,
9x + 152 y = 21
has no solution.
For what value of k, the system of equations
x + 2y = 3,
5x + ky + 7 = 0
Have (i) a unique solution, (ii) no solution?
Also, show that there is no value of k for which the given system of equation has infinitely namely solutions
Find the values of a and b for which the system of linear equations has an infinite number of solutions:
(a – 1) x + 3y = 2, 6x + (1 – 2b)y = 6
The sum of the digits of a two-digit number is 12. The number obtained by interchanging its digits exceeds the given number by 18. Find the number.
The sum of the digits of a two-digit number is 15. The number obtained by interchanging the digits exceeds the given number by 9. Find the number.
A number consists of two digits. When it is divided by the sum of its digits, the quotient is 6 with no remainder. When the number is diminished by 9, the digits are reversed. Find the number.
The sum of a two-digit number and the number obtained by reversing the order of its digits is 121, and the two digits differ by 3. Find the number,
The sum of the numerator and denominator of a fraction is 8. If 3 is added to both of the numerator and the denominator, the fraction becomes `3/4`. Find the fraction.
Places A and B are 160 km apart on a highway. A car starts from A and another car starts from B simultaneously. If they travel in the same direction, they meet in 8 hours. But, if they travel towards each other, they meet in 2 hours. Find the speed of each car.
Write the number of solutions of the following pair of linear equations:
x + 2y -8=0,
2x + 4y = 16
Find the value of k for which the system of equations 2x + 3y -5 = 0 and 4x + ky – 10 = 0 has infinite number of solutions.
Solve for x:
3x2-2x-83=0
Solve the following for x:
`1/(2a+b+2x)=1/(2a)+1/b+1/(2x)`
Find the value(s) of p in (i) to (iv) and p and q in (v) for the following pair of equations:
3x – y – 5 = 0 and 6x – 2y – p = 0,
if the lines represented by these equations are parallel.
A pair of linear equations which has a unique solution x = 2, y = –3 is ______.
