Advertisements
Advertisements
Question
The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically.
Solution
Let cost of one bat = Rs x
Cost of one ball = Rs y
3 bats and 6 balls for Rs 3900 So that
3x + 6y = 3900
Dividing equation by 3, we get
x + 3y = 1300
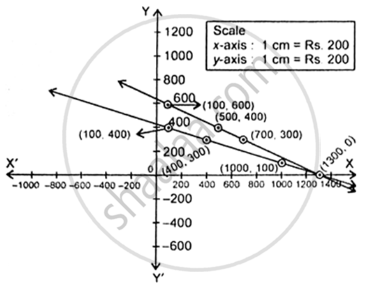
Graphical representation:
we have,
3x + 6y = 3900
3(x + 2y) = 3900
x + 2y = 1300
a = 1300 - 2y
Thus, we have following table:
| x | 1300 | 500 | 700 | 100 |
| y | 0 | 400 | 300 | 600 |
we have, x + 3y = 1300
x = 1300 - 3y
Thus, we have following table:
| x | 1300 | 100 | 400 | 1000 |
| y | 0 | 400 | 300 | 100 |
when we plot the graph of equations, we find that both the lines intersect at the point (1300, 0).
Therefore, a = 1300, y = 0 is the solution of the given system of equations.
RELATED QUESTIONS
Find the value of k for which each of the following system of equations have no solution
x + 2y = 0
2x + ky = 5
Prove that there is a value of c (≠ 0) for which the system
6x + 3y = c - 3
12x + cy = c
has infinitely many solutions. Find this value.
For what value of k, the following system of equations will represent the coincident lines?
x + 2y + 7 = 0
2x + ky + 14 = 0
Find the values of a and b for which the following system of equations has infinitely many solutions:
2x + 3y = 7
(a - b)x + (a + b)y = 3a + b - 2
Find the values of a and b for which the following system of equations has infinitely many solutions:
2x + 3y = 7
(a - 1)x + (a + 1)y = (3a - 1)
Solve for x and y:
`2x - 3/y = 9, 3x + 7/y = 2`
Solve for x and y:
`3/x - 1/y + 9 = 0, 2/x + 3/y = 5`
Solve for x and y:
x + y = 5xy, 3x + 2y = 13xy
Solve for x and y:
`3/(x+y) + 2/(x−y)= 2, 3/(x+y) + 2/(x−y) = 2`
Solve for x and y:
`44/(x+y) + 30/(x−y) = 10, 55/(x+y) - 40/(x−y) = 13`
Solve for x and y:
217x + 131y = 913, 131x + 217y = 827
Solve for x and y:
23x - 29y = 98, 29x - 23y = 110
Solve for x and y:
`x/a + y/b = 2, ax – by = (a^2 – b^2)`
Solve for x and y:
`x + y = a + b, ax - by = a^2 - b^2`
Solve for x and y:
`x/a + y/b = a + b, x/(a^2)+ y/(b^2) = 2`
Show that the following system of equations has a unique solution:
`x/3 + y/2 = 3, x – 2y = 2.`
Also, find the solution of the given system of equations.
Find the value of k for which the system of linear equations has an infinite number of solutions:
2x + 3y = 7,
(k – 1)x + (k + 2)y = 3k.
A sailor goes 8 km downstream in 420 minutes and returns in 1 hour. Find the speed of the sailor in still water and the speed of the current .
2 men and 5 boys can finish a piece of work in 4 days, while 3 men and 6 boys can finish it in 3 days. Find the time taken by one man alone to finish the work and that taken by one boy alone to finish the work.
The area of a rectangle gets reduced by `8m^2`, when its length is reduced by 5m and its breadth is increased by 3m. If we increase the length by 3m and breadth by 2m, the area is increased by `74m^2`. Find the length and the breadth of the rectangle.
Five years hence, a man’s age will be three times the sum of the ages of his son. Five years ago, the man was seven times as old as his son. Find their present ages
If twice the son’s age in years is added to the mother’s age, the sum is 70 years. But, if twice the mother’s age is added to the son’s age, the sum is 95 years. Find the age of the mother and that of the son.
On selling a tea-set at 5% loss and a lemon-set at 15% gain, a shopkeeper gains Rs. 7. However, if he sells the tea-set at 5% gain and the lemon-set at 10% gain, he gains Rs. 14. Find the price of the tea-set and that of the lemon-set paid by the shopkeeper.
Write the number of solutions of the following pair of linear equations:
x + 2y -8=0,
2x + 4y = 16
Find the values of k for which the system of equations 3x + ky = 0,
2x – y = 0 has a unique solution.
Find the value of k for which the system of equations x + 2y – 3 = 0 and 5x + ky + 7 = 0 is inconsistent.
Solve for x:
Solve the following pair of linear equations:
3x − 5y = 4
2y + 7 = 9x
Find the value(s) of p in (i) to (iv) and p and q in (v) for the following pair of equations:
3x – y – 5 = 0 and 6x – 2y – p = 0,
if the lines represented by these equations are parallel.
Read the following passage:
|
A coaching institute of Mathematics conducts classes in two batches I and II and fees for rich and poor children are different. In batch I, there are 20 poor and 5 rich children, whereas in batch II, there are 5 poor and 25 rich children. The total monthly collection of fees from batch I is ₹9,000 and from batch II is ₹26,000. Assume that each poor child pays ₹x per month and each rich child pays ₹y per month.
|
Based on the above information, answer the following questions:
- Represent the information given above in terms of x and y.
- Find the monthly fee paid by a poor child.
OR
Find the difference in the monthly fee paid by a poor child and a rich child. - If there are 10 poor and 20 rich children in batch II, what is the total monthly collection of fees from batch II?

