Advertisements
Advertisements
प्रश्न
The difference in the frequencies of series limit of Lyman series and Balmer series is equal to the frequency of the first line of the Lyman series. Explain.
उत्तर
The 'series limit' refers to the 'shortest wavelength' (corresponding to the maximum photon energy).
The frequency of the radiation emitted for transition from n1 to n2 is given by
`f = k (1/n_1^2 - 1/n_2^2)`
Here, k is a constant.
For the series limit of Lyman series,
`n_1 = 1`
`n_2 = ∞`
Frequency, `f_1 = k( 1/1^2 - 1/∞ ) = k`
For the first line of Lyman series,
`n_1 = 1`
`n_2 = 2`
Frequency, `f_2 = k(1/1^2 - 1/2^2) = (3k)/4`
For series limit of Balmer series,
`n_1 = 2`
`n_2 = ∞ `
`f_1 = k(1/2^2 - 1 /∞) = k/4`
`f_1 - f_3 = f_2`
Thus, the difference in the frequencies of series limit of Lyman series and Balmer series is equal to the frequency of the first line of the Lyman series.
APPEARS IN
संबंधित प्रश्न
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
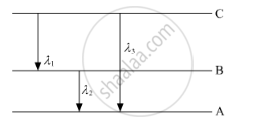
Using Bohr's postulates of the atomic model, derive the expression for radius of nth electron orbit. Hence obtain the expression for Bohr's radius.
The energy associated with the first orbit in the hydrogen atom is - 2.18 × 10-18 J atom-1. What is the energy associated with the fifth orbit?
Calculate the radius of Bohr’s fifth orbit for hydrogen atom
In Bohr’s model of the hydrogen atom, the radius of the first orbit of an electron is r0 . Then, the radius of the third orbit is:
a) `r_0/9`
b) `r_0`
c) `3r_0`
d) `9r_0`
Using Bohr's postulates, derive the expression for the total energy of the electron in the stationary states of the hydrogen atom ?
A positive ion having just one electron ejects it if a photon of wavelength 228 Å or less is absorbed by it. Identify the ion.
A beam of light having wavelengths distributed uniformly between 450 nm to 550 nm passes through a sample of hydrogen gas. Which wavelength will have the least intensity in the transmitted beam?
Light from Balmer series of hydrogen is able to eject photoelectrons from a metal. What can be the maximum work function of the metal?
The earth revolves round the sun due to gravitational attraction. Suppose that the sun and the earth are point particles with their existing masses and that Bohr's quantization rule for angular momentum is valid in the case of gravitation. (a) Calculate the minimum radius the earth can have for its orbit. (b) What is the value of the principal quantum number n for the present radius? Mass of the earth = 6.0 × 10−24 kg. Mass of the sun = 2.0 × 1030 kg, earth-sun distance = 1.5 × 1011 m.
Answer the following question.
Use Bohr's model of hydrogen atom to obtain the relationship between the angular momentum and the magnetic moment of the revolving electron.
Mention demerits of Bohr’s Atomic model.
For an electron in the second orbit of hydrogen, what is the moment of momentum as per the Bohr's model?
The energy of an electron in hth orbit of hydrogen atom is –13.6/n2ev energy required to excite the electron from the first orbit to the third orbit is
According to Bhor' s theory the moment of momentum of an electron revolving in second orbit of hydrogen atom will be.
A set of atoms in an excited state decays ______.
The wavelength in Å of the photon that is emitted when an electron in Bohr orbit with n = 2 returns to orbit with n = 1 in H atom is ______ Å. The ionisation potential of the ground state of the H-atom is 2.17 × 10−11 erg.
What is the energy of an electron in stationary state corresponding to n = 2?
Write the ionisation energy value for the hydrogen atom.
State three postulates of Bohr's theory of hydrogen atom.
