Advertisements
Advertisements
प्रश्न
The distance between the points (0, 5) and (–3, 1) is ______.
विकल्प
8 units
5 units
3 units
25 units
उत्तर
The distance between the points (0, 5) and (–3, 1) is 5 units.
Explanation:
Let be point A(0, 5) and B(–3, 1)
x1 = 0, y1 = 5, x2 = –3, y2 = 1
Distance between the points
AB = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
AB = `sqrt((-3 - 0)^2 + (1 - 5)^2`
= `sqrt(9 + 16)`
= `sqrt(25)`
= 5 units
APPEARS IN
संबंधित प्रश्न
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b). Prove that bx = ay.
Show that the points (1, – 1), (5, 2) and (9, 5) are collinear.
If the distances of P(x, y) from A(5, 1) and B(–1, 5) are equal, then prove that 3x = 2y
AB and AC are the two chords of a circle whose radius is r. If p and q are
the distance of chord AB and CD, from the centre respectively and if
AB = 2AC then proove that 4q2 = p2 + 3r2.
Prove that the points A (1, -3), B (-3, 0) and C (4, 1) are the vertices of an isosceles right-angled triangle. Find the area of the triangle.
Show that (-3, 2), (-5, -5), (2, -3) and (4, 4) are the vertices of a rhombus.
Show that A(1, 2), (1, 6), C(1 + 2 `sqrt(3)`, 4) are vertices of a equilateral triangle
What is the distance of the point (– 5, 4) from the origin?
Find the distance between the points O(0, 0) and P(3, 4).
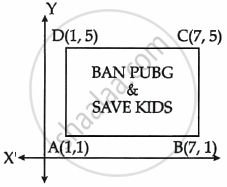
Read the following passage:
|
Use of mobile screen for long hours makes your eye sight weak and give you headaches. Children who are addicted to play "PUBG" can get easily stressed out. To raise social awareness about ill effects of playing PUBG, a school decided to start 'BAN PUBG' campaign, in which students are asked to prepare campaign board in the shape of a rectangle: One such campaign board made by class X student of the school is shown in the figure.
|
Based on the above information, answer the following questions:
- Find the coordinates of the point of intersection of diagonals AC and BD.
- Find the length of the diagonal AC.
-
- Find the area of the campaign Board ABCD.
OR - Find the ratio of the length of side AB to the length of the diagonal AC.
- Find the area of the campaign Board ABCD.