Advertisements
Advertisements
प्रश्न
The floor of a room is of size 6 m x 5 m. Find the cost of covering the floor of the room with 50 cm wide carpet at the rate of Rs.24.50 per metre. Also, find the cost of carpeting the same hall if the carpet, 60 cm, wide, is at the rate of Rs.26 per metre.
उत्तर
Area of floor of a room
= 6m x 5m
= 30m2
Let the length of the carpet that is 50cm wide be l m.
∴ Area of carpet
= length x breadth
= l m x 50cm
= l x 0.5m2
Since area of carpet
= Area of floor of a room
⇒ l x 0.5 = 30
⇒ l `(30)/(0.5)`
= 60m
∴ Cost of carpet at Rs.24.50per mate
= Rs.60 x 24.50
= Rs.1470
Let the length of the carpet that is 60cm wide be L m.
∴ Area of carpet
= length x breadth
= l m x 60cm
= l x 0.6m2
Since area of carpet
= Area of floor of a room
⇒ l x 0.6 = 30
⇒ l `(30)/(0.6)`
= 50m
∴ Cost of carpet at Rs.26per mate
= Rs.50 x 26
= Rs.1300.
APPEARS IN
संबंधित प्रश्न
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Trapezium given below; find its area.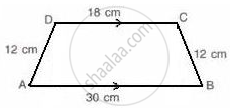
The cost of enclosing a rectangular garden with a fence all around, at the rate of 75 paise per metre, is Rs. 300. If the length of the garden is 120 metres, find the area of the field in square metres.
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
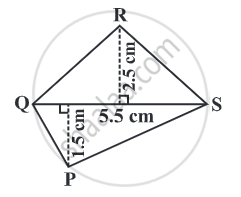
Find the area of quadrilateral PQRS.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (0, 0), (p, 8), (6, 2) | 20 |
In the following, find the value of ‘a’ for which the given points are collinear
(2, 3), (4, a) and (6, – 3)
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
