Advertisements
Advertisements
प्रश्न
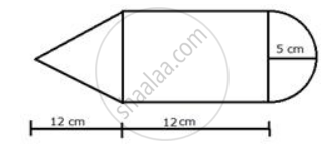
The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. This common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.

उत्तर
The volume of solid = Volume of cone + Volume of cylinder + Volume of the hemisphere.
Volume of cone = `(pir^2h)/3 = (22xx7xx7xx4)/(7xx3) = 616/3 cm^3`
Volume of cylinder = `pir^2h = (22xx7xx7xx4)/7 = 616 cm^3`
Volume of hemisphere = `2/3pir^3 = (2xx22xx7xx7xx7)/(3xx7) =2156/3 cm^3`
Total volume = `616/3 + 616 + 2156/3 = 1540 cm^3`
APPEARS IN
संबंधित प्रश्न
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
`["Assume "pi=22/7]`
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
`["Assume "pi=22/7]`
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
- radius of the base and
- total surface area of the cone.
`["Assume "pi =22/7]`
The radius and slant height of a cone are In the ratio of 4 : 7. If its curved surface area is 792 cm2, find its radius. (Use it 𝜋 = 22/7).
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m
wide to make the required tent.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm (Use it 𝜋 = 3.14)
A bus stop is barricated from the remaining part of the road, by using 50 hollow cones made of recycled card-board. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m2, what will be the cost of painting all these cones. (Use 𝜋 = 3.14 and √1.04 = 1.02)
The radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cubic meter, find the slant height and the radius (Use it 𝜋 = 3.14).
The radii of the bases of two solid right circular cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms r1, r2 and R.
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter 14 cm and height 8 cm. Find the number of cones so formed.
Find the radius of the circular base of the cone , if its volume is 154 cm3 and the perpendicular height is 12 cm
The heights of two cones are in the ratio 1:3 and their base radii are in the ratio 3:1. Find the ratio of their volumes.
Find the height of the cone whose base radius is 5 cm and volume is 75π cm3.
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
