Advertisements
Advertisements
प्रश्न
The following table gives the characteristics of the project
| Activity | 1 - 2 | 1 - 3 | 2 - 3 | 3 - 4 | 3 - 5 | 4 - 6 | 5 - 6 | 6 - 7 |
| Duration (in days) |
5 | 10 | 3 | 4 | 6 | 6 | 5 | 5 |
Draw the network for the project, calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and find the critical path. Compute the project duration.
उत्तर
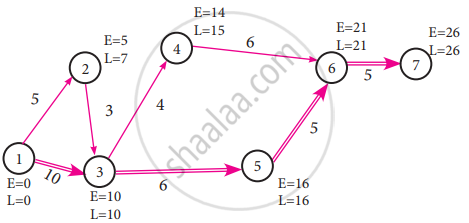
E1 = 0
E2 = 0 + 5 = 5
E3 = (5 + 3) or (0 + 10)
Whichever is maximum
= 10
E4 = 10 + 4 = 14
E5 = 10 + 6 = 16
E6 = (14 + 6) or (16 + 5)
Whichever is maximum
= 21
E7 = 21 + 5 = 26
L7 = 26
L6 = 26 − 5 = 21
L5 = 21 − 5 = 16
L4 = 21 − 6 = 15
L3 = (15 − 4) or (16 − 6)
Whichever is minimum
= 10
L2 = 10 − 3 = 7
L1 = (7 − 5) or (10 − 10)
Whichever is minimum
L1 = 0
| Activity | Duration tij |
EST | EFT = EST + tij | LST = LFT – tij | LFT |
| 1 - 2 | 5 | 0 | 5 | 7 − 5 = 2 | 7 |
| 1 - 3 | 10 | 0 | 10 | 10 − 10 = 0 | 10 |
| 2 - 3 | 3 | 5 | 8 | 10 − 3 = 7 | 10 |
| 3 - 4 | 4 | 10 | 14 | 15 − 4 = 11 | 15 |
| 3 - 5 | 6 | 10 | 16 | 16 − 6 = 10 | 16 |
| 4 - 6 | 6 | 14 | 20 | 21 − 6 = 15 | 21 |
| 5 - 6 | 5 | 16 | 21 | 21 − 5 = 16 | 21 |
| 6 - 7 | 5 | 21 | 26 | 26 − 5 = 21 | 26 |
Since EFT and LFT values are same in 1 - 3, 3 - 5, 5 - 6 and 6 - 7.
Hence the critical path is 1 - 3 - 5 - 6 - 7 and the duration of time taken is 26 days.
APPEARS IN
संबंधित प्रश्न
Draw the event oriented network for the following data:
| Events | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Immediate Predecessors | - | 1 | 1 | 2, 3 | 3 | 4, 5 | 5, 6 |
Construct the network for the projects consisting of various activities and their precedence relationships are as given below:
A, B, C can start simultaneously A < F, E; B < D, C; E, D < G
A project schedule has the following characteristics
| Activity | 1 - 2 | 1 - 3 | 2 - 4 | 3 - 4 | 3 - 5 | 4 - 9 | 5 - 6 | 5 - 7 | 6 - 8 | 7 - 8 | 8 - 10 | 9 - 10 |
| Time | 4 | 1 | 1 | 1 | 6 | 5 | 4 | 8 | 1 | 2 | 5 | 7 |
Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
The following table gives the activities of a project and their duration in days
| Activity | 1 - 2 | 1 - 3 | 2 - 3 | 2 - 4 | 3 - 4 | 3 - 5 | 4 - 5 |
| Duration | 5 | 8 | 6 | 7 | 5 | 4 | 8 |
Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
One of the conditions for the activity (i, j) to lie on the critical path is
In a network while numbering the events which one of the following statements is false?
In the context of network, which of the following is not correct
The objective of network analysis is to
Draw a network diagram for the following activities.
| Activity code | A | B | C | D | E | F | G | H | I | J | K |
| Predecessor activity | - | A | A | A | B | C | C | C, D | E, F | G, H | I, J |
A Project has the following time schedule
| Activity | 1 - 2 | 2 - 3 | 2 - 4 | 3 - 5 | 4 - 6 | 5 - 6 |
| Duration (in days) |
6 | 8 | 4 | 9 | 2 | 7 |
Draw the network for the project, calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and find the critical path. Compute the project duration.
