Advertisements
Advertisements
प्रश्न
The line `(3x)/5 - (2y)/3 + 1 = 0` contains the point (m, 2m – 1); calculate the value of m.
उत्तर
The equation of the given line is `(3x)/5 - (2y)/3 + 1 = 0`
Putting x = m, y = 2m − 1, we have:
`(3m)/5 - (2(2m - 1))/3 + 1 = 0`
`(3m)/5 - (4m - 2)/3 + 1 = 0`
`(9m - 20m + 10)/15 = -1`
9m – 20m + 10 = –15
–11m = –25
`m = 25/11 = 2 3/11`
APPEARS IN
संबंधित प्रश्न
A(2, 5), B(–1, 2) and C(5, 8) are the vertices of a triangle ABC, `M' is a point on AB such that AM: MB = 1: 2. Find the coordinates of 'M'. Hence find the equation of the line passing through the points C and M
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the co-ordinates of the point where PQ intersects the x-axis.
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
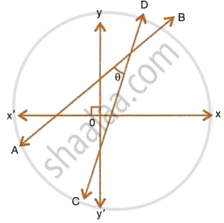
Write down the equation of the line whose gradient is `3/2` and which passes through P, where P divides the line segment joining A(−2, 6) and B(3, −4) in the ratio 2 : 3.
Find if the following points lie on the given line or not:
(-1, 5) on the line 3x = 2y -15
The line 2x - 5y + 31 = 0 bisects the join of (-4,5) and (P, 9). Find the value of p.
The coordinates of two points P and Q are (0,4) and (3,7) respectively. Find
(i) The gradient of PQ
(ii) the equation of PQ
(iii) the coordinates of the point where the line AB intersects the X-axis.
Find the equation of the straight line which has Y-intercept equal to 4/3 and is perpendicular to 3x – 4y + 11 = 0.
In the adjoining figure, write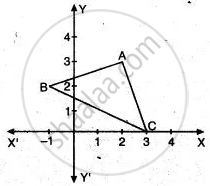
(i) The coordinates of A, B and C.
(ii) The equation of the line through A and | | to BC.
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
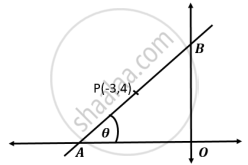
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
