Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The minute hand of clock is10cm long. Find the area of the face of the clock described by the minute hand between 8am and 8:25 am
рдЙрддреНрддрд░
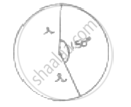
Radius of minute hand (r) = 10 cm
For 1 hr = 60 min, minute hand completes one revolution = 360°
60 min = 360°
1 min = 6°
From 8 am to 8:25 am it is 25 min angle subtended = 6° × 25 = 150° = ЁЭЬГ
Area described =`theta/360^@× pir^2`
=`150/360×22/7`× 10 × 10
=`(250×11)/3`
=`2750/3 cm^2`
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
A car has wheels which are 80 cm in diameter. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour ?
An arc of a circle is of length 5π cm and the sector it bounds has an area of 20 π cm2. Find the radius of the circle.
The base of a right – angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
Choose the correct alternative answer for the following question.
The curved surface area of a cylinder is 440 cm 2 and its radius is 5 cm. Find its height.
Diagonal of a square is 20 cm. Find the length and perimeter of the square.
The perimeter of a square and the circumference of a circle are equal. If the length of each side of the square is 22 cm, find:
(i) perimeter of the square.
(ii) circumference of the circle.
(iii) radius of the circle.
The diameter of the wheel of a cart is 1.05 m. How much distance will the cart cover in 1000 rotations of the wheel?
Formula used to find the circumference of a circle is
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
Circumference ‘C’ of a circle is equal to 2π × ______.
