Advertisements
Advertisements
प्रश्न
The minute hand of a clock is √21 𝑐𝑚 long. Find area described by the minute hand on the face of clock between 7 am and 7:05 am
उत्तर
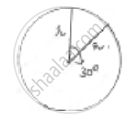
Radius of minute hand (r) = √21 𝑐𝑚
For 1hr = 60 min, minute hand completes one revolution = 360°
60 min = 360°
1 min = 6°
From 7 am to 7:05 am it is 5 min angle subtended = 5 × 6° = 30° = 𝜃
Area described =`theta/360^@ × pir^2`
=`30/360×22/7`× 21
=`22/4`= 5.5 cm2
APPEARS IN
संबंधित प्रश्न
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)

A horse is tied to a pole with 28m long string. Find the area where the horse can graze.
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
A wire bent in the form of an equilateral triangle has an area of 121 `sqrt 3` cm2. If the same wire is bent into the form of a circle , find the area enclosed by the wire.
Find the circumference of the circle whose area is 25 times the area of the circle with radius 7 cm.
Find the area and perimeter of the following semi-circle :
Radius= 1.4 cm
Find the area and perimeter of the following sector :
Radius= 6 cm, angle at the centre is 70°
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles.
In Figure 2, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region.

The circumferences of two circles are in the ratio 5: 7, find the ratio between their radius.
