Advertisements
Advertisements
प्रश्न
The speed-time graph of an ascending passenger lift is given alongside. What is the acceleration of the lift:
(1) during the first two seconds ?
(2) between second and tenth second ?
(3) during the last two seconds ?
उत्तर
(i) We have to find the acceleration from the given graph.
Acceleration = slope of line AB
= `((4.6-0))/((2-0)) "m/s"^2`
= 2.3 `"m/s"^2`
(ii) Between second and tenth second, it represents uniform speed, so, acceleration acting on the lift is zero.
(iii) During the last two seconds, it represents retardation of the lift, so its acceleration is (–2.3 m/s2).
APPEARS IN
संबंधित प्रश्न
What does the slope of a speed-time graph indicate ?
Study the speed-time graph of a car given alongside and answer the following questions:

(i) What type of motion is represented by OA ?
(ii) What type of motion is represented by AB ?
(iii) What type of motion is represented by BC ?
(iv) What is the acceleration of car from O to A ?
(v)What is the acceleration of car from A to B ?
(vi) What is the retardation of car from B to C ?
From the displacement-time graph of a cyclist given below in the Figure, find The time after which he reaches the starting point .

Multiple choice Question. Select the correct option.
What does the area of an acceleration – time graph represent?
From the velocity – time graph given below, calculate acceleration in the region AB.

From the velocity – time graph given below, calculate Distance covered in the region ABCE.

Draw velocity-time graph to show:
Acceleration
Write a sentence to explain the shape of graph.
Sketch the shape of the velocity-time graph for a body moving with:
Uniformly velocity
Figure shows the distance-time graph of three students A, B and C. On the basis of the graph, answer the following :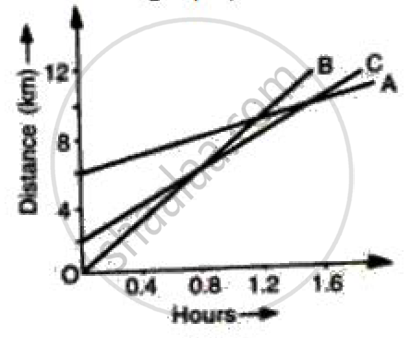
How far did B travel between the time he passed C and A?
State whether true or false. If false, correct the statement.
If the velocity – time graph of a particle is a straight line inclined to X-axis then its displacement – time graph will be a straight line.
