Advertisements
Advertisements
प्रश्न
The temperature and humidity of air are 27°C and 50% on a particular day. Calculate the amount of vapour that should be added to 1 cubic metre of air to saturate it. The saturation vapour pressure at 27°C = 3600 Pa.
Use R = 8.3 J K-1 mol-1
उत्तर
Here ,
SVP = 3600 Pa
T = 273 + 27 = 300K
`"V" = 1 "m"^3`
M = 18 g for water
RH = 50%
⇒ `(VP)/(SVP) = 0.5`
⇒ `"VP" = 0.5 xx 3600 = 1800`
Let m1 be the mass of water present in the 50% humid air.
PV = nRT
⇒`PV = m_1/MRT`
⇒ `1800 = "m"_1/18 xx 8.3 xx 300`
⇒ `"m"_1` = 13 g
Required pressure for saturation = 3600 Pa
Let `"m"_2` be the amount of water required for saturation .
⇒ 3600 = `"m"_2/M`RT
⇒ `"m"_2` = `(3600 xx 18)/(8.3 xx 300)` = 26g
Total excess water vapour that has to be added = `"m"_2 - "m"_1`
⇒ 36 - 13 = 13 g
APPEARS IN
संबंधित प्रश्न
From a certain apparatus, the diffusion rate of hydrogen has an average value of 28.7 cm3 s–1. The diffusion of another gas under the same conditions is measured to have an average rate of 7.2 cm3 s–1. Identify the gas
[Hint: Use Graham’s law of diffusion: R1/R2 = (M2/M1)1/2, where R1, R2 are diffusion rates of gases 1 and 2, and M1 and M2 their respective molecular masses. The law is a simple consequence of kinetic theory.]
Figure shows graphs of pressure vs density for an ideal gas at two temperatures T1 and T2.
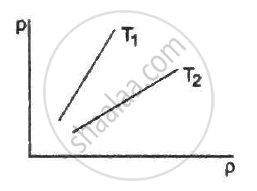
The pressure of a gas kept in an isothermal container is 200 kPa. If half the gas is removed from it, the pressure will be
Equal masses of air are sealed in two vessels, one of volume V0 and the other of volume 2V0. If the first vessel is maintained at a temperature 300 K and the other at 600 K, find the ratio of the pressures in the two vessels.
Use R = 8.31 JK-1 mol-1
Figure shows a cylindrical tube with adiabatic walls and fitted with a diathermic separator. The separator can be slid in the tube by an external mechanism. An ideal gas is injected into the two sides at equal pressures and equal temperatures. The separator remains in equilibrium at the middle. It is now slid to a position where it divides the tube in the ratio of 1:3. Find the ratio of the pressures in the two parts of the vessel.
Use R=8.314J K-1 mol-1

An air bubble of radius 2.0 mm is formed at the bottom of a 3.3 m deep river. Calculate the radius of the bubble as it comes to the surface. Atmospheric pressure = 1.0 × 105 Pa and density of water = 1000 kg m−3.
A vessel contains 1.60 g of oxygen and 2.80 g of nitrogen. The temperature is maintained at 300 K and the volume of the vessel is 0.166 m3. Find the pressure of the mixture.
Use R = 8.3 J K-1 mol-1
Is a slow process always isothermal? Is a quick process always adiabatic?
A vessel of volume V0 contains an ideal gas at pressure p0 and temperature T. Gas is continuously pumped out of this vessel at a constant volume-rate dV/dt = r keeping the temperature constant. The pressure of the gas being taken out equals the pressure inside the vessel. Find (a) the pressure of the gas as a function of time, (b) the time taken before half the original gas is pumped out.
Use R = 8.3 J K−1 mol−1
A gas is enclosed in a cylindrical can fitted with a piston. The walls of the can and the piston are adiabatic. The initial pressure, volume and temperature of the gas are 100 kPa, 400 cm3 and 300 K, respectively. The ratio of the specific heat capacities of the gas, Cp / Cv = 1.5. Find the pressure and the temperature of the gas if it is (a) suddenly compressed (b) slowly compressed to 100 cm3.
The initial pressure and volume of a given mass of a gas (Cp/Cv = γ) are p0 and V0. The gas can exchange heat with the surrounding. (a) It is slowly compressed to a volume V0/2 and then suddenly compressed to V0/4. Find the final pressure. (b) If the gas is suddenly compressed from the volume V0 to V0/2 and then slowly compressed to V0/4, what will be the final pressure?
A barometer correctly reads the atmospheric pressure as 76 cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then becomes constant. If the saturation vapour pressure at the atmospheric temperature is 0.80 cm of mercury, find the height of the mercury column when it reaches its minimum value.
The temperature and relative humidity in a room are 300 K and 20% respectively. The volume of the room is 50 m3. The saturation vapour pressure at 300 K 3.3 kPa. Calculate the mass of the water vapour present in the room.
Use R = 8.3 J K-1 mol-1
The temperature and the relative humidity are 300 K and 20% in a room of volume 50 m3. The floor is washed with water, 500 g of water sticking on the floor. Assuming no communication with the surrounding, find the relative humidity when the floor dries. The changes in temperature and pressure may be neglected. Saturation vapour pressure at 300 K = 3.3 kPa.
Use R = 8.31 J K-1 mol-1
A bucket full of water is placed in a room at 15°C with initial relative humidity 40%. The volume of the room is 50 m3. (a) How much water will evaporate? (b) If the room temperature is increased by 5°C, how much more water will evaporate? The saturation vapour pressure of water at 15°C and 20°C are 1.6 kPa and 2.4 kPa respectively.
Use R = 8.3 J K-1 mol-1
If 1022 gas molecules each of mass 10-26 kg collide with a surface (perpendicular to it) elastically per second over an area of 1 m2 with a speed of 104 m/s, the pressure exerted by the gas molecules will be of the order of ______.
Air separated from the atmosphere by a column of mercury of length h = 15 cm is present in a narrow cylindrical two-soldered at one end. When the tube is placed horizontally the air occupies a volume V1 = 240 mm3. When it is set vertically with its open end upwards the volume of the air is V2 = 200 mm3. The atmospheric pressure during the experiment is 7n cm of Hg where n is a single digit number. n will be ______.
