Advertisements
Advertisements
प्रश्न
The temperature of a wire is doubled. The Young’s modulus of elasticity ______.
विकल्प
will also double.
will become four times.
will remain same.
will decrease.
उत्तर
The temperature of a wire is doubled. The Young’s modulus of elasticity will decrease.
Explanation:
Young's modulus (Y): It is defined as the ratio of normal stress to longitudinal strain within the limit of proportionality.
`Y = "Normal stress"/"Longitudinal strain"`
= `(F/A)/((ΔL)/L)`
= `(FL)/(AΔL)`
The fractional change in length of any material is defined as `(ΔL)/L_0 = αΔT` where ΔT is the change in the temperature, L0 is the original length, α is the coefficient of linear expansion of the given material and L0 is the original length of material.
So, simply a change in length is due to change in temperature.
`ΔL = L_0αΔT`
And Young's modules
(Y) = `"Stress"/"Strain"`
= `(FL_0)/(A xx ΔL)`
= `(FL_0)/(AL_0 ΔT) ∝ 1/(ΔT)`
As Y ∝ 1/∆T
When temperature increases ∆T increases, hence Y decreases.
APPEARS IN
संबंधित प्रश्न
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10–5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10–5 m2 under a given load. What is the ratio of Young’s modulus of steel to that of copper?
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.

Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner and outer radii of each column are 30 cm and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
Two wires A and B are made of same material. The wire A has a length l and diameter rwhile the wire B has a length 2l and diameter r/2. If the two wires are stretched by the same force, the elongation in A divided by the elongation in B is
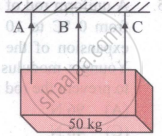
A uniform rectangular block of mass of 50 kg is hung horizontally with the help of three wires A, B and C each of length and area of 2m and 10mm2 respectively as shown in the figure. The central wire is passing through the centre of gravity and is made of material of Young's modulus 7.5 x 1010 Nm−2 and the other two wires A and C symmetrically placed on either side of the wire B are of Young's modulus 1011 Nm−2 The tension in the wires A and B will be in the ratio of:
What is the Young’s modulus for a perfect rigid body ?
A truck is pulling a car out of a ditch by means of a steel cable that is 9.1 m long and has a radius of 5 mm. When the car just begins to move, the tension in the cable is 800 N. How much has the cable stretched? (Young’s modulus for steel is 2 × 1011 Nm–2.)
A steel wire of mass µ per unit length with a circular cross section has a radius of 0.1 cm. The wire is of length 10 m when measured lying horizontal, and hangs from a hook on the wall. A mass of 25 kg is hung from the free end of the wire. Assuming the wire to be uniform and lateral strains << longitudinal strains, find the extension in the length of the wire. The density of steel is 7860 kg m–3 (Young’s modules Y = 2 × 1011 Nm–2).
If the yield strength of steel is 2.5 × 108 Nm–2, what is the maximum weight that can be hung at the lower end of the wire?
In nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by `(Ypir^4)/(4R) . Y` is the Young’s modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
