Advertisements
Advertisements
प्रश्न
The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seoul Olympics in 1988, setting a new Olympic record of 10⋅54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be 50 kg. Calculate the kinetic energy of Griffith-Joyner at her full speed.
उत्तर
Given:
Distance covered by her, s = 100 m
Time taken by her to cover 100 m, t = 10.54 s
Mass, m = 50 kg
The motion can be assumed to be uniform.
\[\text{ Speed } , \nu = \frac{s}{t} = 9 . 487 \text{ m/s } \]
\[\text{ So, K . E } . = \frac{1}{2} {m\nu}^2 = 2250 J\]
APPEARS IN
संबंधित प्रश्न
Is work-energy theorem valid in non-inertial frames?
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. what are the initial and final kinetic energies of the ball?
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. What is the work done by the kinetic friction?
The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seoul Olympics in 1988, setting a new Olympic record of 10⋅54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be 50 kg. What power Griffith-Joyner had to exert to maintain uniform speed?
A block of mass 30 kg is being brought down by a chain. If the block acquires a speed of 40 cm/s in dropping down 2 m, find the work done by the chain during the process.
Consider the situation shown in the following figure. The system is released from rest and the block of mass 1 kg is found to have a speed 0⋅3 m/s after it has descended a distance of 1 m. Find the coefficient of kinetic friction between the block and the table.
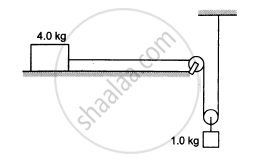
A block of mass 100 g is moved with a speed of 5⋅0 m/s at the highest point in a closed circular tube of radius 10 cm kept in a vertical plane. The cross-section of the tube is such that the block just fits in it. The block makes several oscillations inside the tube and finally stops at the lowest point. Find the work done by the tube on the block during the process.
A small block of mass 200 g is kept at the top of a frictionless incline which is 10 m long and 3⋅2 m high. How much work was required (a) to lift the block from the ground and put it an the top, (b) to slide the block up the incline? What will be the speed of the block when it reaches the ground if (c) it falls off the incline and drops vertically to the ground (d) it slides down the incline? Take g = 10 m/s2.
A block of mass 5 kg is suspended from the end of a vertical spring which is stretched by 10 cm under the load of the block. The block is given a sharp impulse from below, so that it acquires an upward speed of 2 m/s. How high will it rise? Take g = 10 m/s2.
A block of mass 250 g is kept on a vertical spring of spring constant 100 N/m fixed from below. The spring is now compressed 10 cm shorter than its natural length and the system is released from this position. How high does the block rise ? Take g = 10 m/s2.
A heavy particle is suspended by a 1⋅5 m long string. It is given a horizontal velocity of \[\sqrt{57} \text{m/s}\] (a) Find the angle made by the string with the upward vertical when it becomes slack. (b) Find the speed of the particle at this instant. (c) Find the maximum height reached by the particle over the point of suspension. Take g = 10 m/s2.
Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. Assuming that the projection-speed is \[\nu_0\] and that the block does not lose contact with the track before reaching its top, find the force acting on it when it reaches the top.
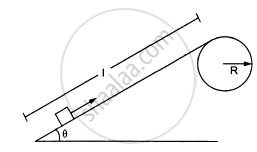
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Find the gravitational potential energy of the chain with reference level at the centre of the sphere.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Find the tangential acceleration \[\frac{d\nu}{dt}\] of the chain when the chain starts sliding down.
An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because ______.
A bullet of mass m fired at 30° to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of bullet after it emerges out of the target?
- The velocity of the bullet will be reduced to half its initial value.
- The velocity of the bullet will be more than half of its earlier velocity.
- The bullet will continue to move along the same parabolic path.
- The bullet will move in a different parabolic path.
- The bullet will fall vertically downward after hitting the target.
- The internal energy of the particles of the target will increase.
A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 ms–1. Calculate
- the loss of P.E. of the drop.
- the gain in K.E. of the drop.
- Is the gain in K.E. equal to a loss of P.E.? If not why.
Take g = 10 ms–2
