Question

The vertices of a triangle are A(3, 4), B(2, 0) and C(1, 6). Find the equations of the line passing through the mid points of sides AB and BC.

Answer 1

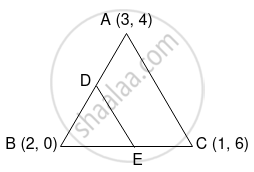
Vertices of ΔABC are A(3, 4), B(2, 0) and C(1, 6).

Let D and E be the midpoints of side AB and side BC respectively.

∴ D = `((3 + 2)/2, (4 + 0)/2) = (5/2, 2)` and

E = `((2 - 1)/2, (0 + 6)/2) = (1/2, 3)`

∴ the equation of the line DE is A(3, 4)

∴ `(y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 - x_1)`

`=> (y - 2)/(3 - 2) = (x - 5/2)/(1/2 - 5/2)`

`=> (y - 2)/1 = ((2x - 5)/2)/((1 - 5)/2)`

`=> (y - 2)/1 = ((2x - 5)/2)/((- 4)/2)`

`=> (y - 2)/1 = (2x - 5)/(-4)`

∴  – 4(y – 2) = 2x – 5

∴  – 4y + 8 = 2x – 5

∴ 2x + 4y – 13 = 0.