Advertisements
Advertisements
प्रश्न
Two charged conducting spheres of radii a and b are connected to each other by a wire. Find the ratio of the electric fields at their surfaces.
उत्तर
Let a be the radius of a sphere A, QA be the charge on the sphere and CA be the capacitance of that sphere. Let b be the radius of a sphere B, QB be the charge on the sphere, and CB be the capacitance of that sphere. Since the two spheres are connected by a wire, their potential (V) will become equal. Let EA be the electric field of sphere A and EB by the electric field of sphere B. Then,
`E_A/E_B = ((Q_A)/(4piε_0a^2)) xx ((b^2 4piε_0)/(Q_B))`
`E_A/E_B = Q_A/Q_B xx b^2/a^2` ......................(i)
However, `Q_A/Q_B = (C_AV)/(C_BV)` .............(ii)
and `C_A/C_B = a/b` ...........(iii)
Putting the values of (ii) and (iii) in (i), we get,
`E_A/E_B = b/a`
Therefore, the required ratio of electric fields at the surface of the spheres is `b/a`.
APPEARS IN
संबंधित प्रश्न
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
Show that there can be no net charge in a region in which the electric field is uniform at all points.
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
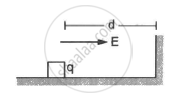
A block of mass containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in the figure. The distance of the block from the wall is d. A horizontal electric field E towards the right is switched on. Assuming elastic collisions (if any), find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?
A uniform electric field of 10 N C−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50 cm.
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
The force per unit charge is known as ______.
