Advertisements
Advertisements
प्रश्न
Two monochromatic beams A and B of equal intensity I, hit a screen. The number of photons hitting the screen by beam A is twice that by beam B. Then what inference can you make about their frequencies?
उत्तर
Effect of intensity: If the intensity of light is increased (while its frequency is kept the same) the current levels off at a higher value, showing that more electrons are being emitted per unit of time. But the stopping potential V0 doesn't change, i.e. Intensity `∝` no . of incident photon no. of emitted photoelectron per time photocurrent.

Effect of frequency: If the frequency of incident light increases, (keeping intensity constant) stopping potential increases but there is no change in photoelectric current.
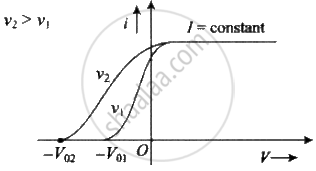
Let us assume nA is the number of photons falling per second of beam A and nB is the number of photons falling per second of beam B.
And it is given that the number of photons hitting the screen by beam A is twice that by beam B.nA = 2nB
The energy of the falling photon of beam A = hvA
The energy of a falling photon of beam B = hvB
Now, according to the question, the intensity of A is equal to the intensity of B.
Therefore, I = nAvA = nBvB
⇒ `v_A/v_B = n_B/n_A = n_B/(2n_B) = 1/2`
⇒ vB = 2vA
APPEARS IN
संबंधित प्रश्न
Define the term 'intensity of radiation' in terms of photon picture of light.
Ultraviolet light of wavelength 2271 Å from a 100 W mercury source irradiates a photo-cell made of molybdenum metal. If the stopping potential is −1.3 V, estimate the work function of the metal. How would the photo-cell respond to a high intensity (∼105 W m−2) red light of wavelength 6328 Å produced by a He-Ne laser?
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1 = 3650 Å, λ2 = 4047 Å, λ3 = 4358 Å, λ4 = 5461 Å, λ5 = 6907 Å,
The stopping voltages, respectively, were measured to be:
V01 = 1.28 V, V02 = 0.95 V, V03 = 0.74 V, V04 = 0.16 V, V05 = 0 V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 × 10−19 C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
Should the energy of a photon be called its kinetic energy or its internal energy?
Planck's constant has the same dimensions as
Calculate the momentum of a photon of light of wavelength 500 nm.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Calculate the number of photons emitted per second by a 10 W sodium vapour lamp. Assume that 60% of the consumed energy is converted into light. Wavelength of sodium light = 590 nm
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In an experiment on photoelectric effect, the stopping potential is measured for monochromatic light beams corresponding to different wavelengths. The data collected are as follows:-
Wavelength (nm): 350 400 450 500 550
Stopping potential (V): 1.45 1.00 0.66 0.38 0.16
Plot the stopping potential against inverse of wavelength (1/λ) on a graph paper and find (a) Planck's constant (b) the work function of the emitter and (c) the threshold wavelength.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A small piece of cesium metal (φ = 1.9 eV) is kept at a distance of 20 cm from a large metal plate with a charge density of 1.0 × 10−9 C m−2 on the surface facing the cesium piece. A monochromatic light of wavelength 400 nm is incident on the cesium piece. Find the minimum and maximum kinetic energy of the photoelectrons reaching the large metal plate. Neglect any change in electric field due to the small piece of cesium present.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In photoelectric effect the photo current ______.
