Advertisements
Advertisements
प्रश्न
Use the graphical method to find the value of k, if:
(5, k - 2) lies on the straight line x - 2y + 1 = 0
उत्तर
x - 2y + 1 = 0
⇒ 2y = x + 1
⇒ y = `(x + 1)/(2)`
The table for x - 2y + 1 = 0 is
| X | 1 | 3 | 5 |
| Y | 1 | 2 | 3 |
Plotting the above points in a graph, we get the following graph:
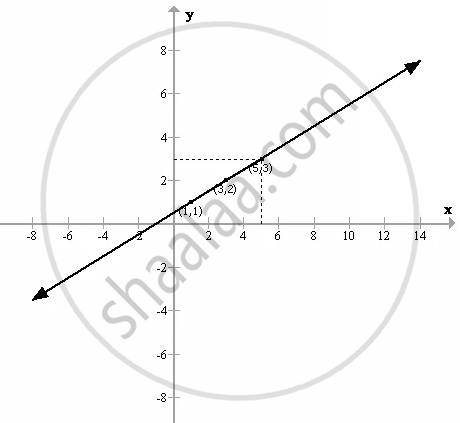
From the above graph, it is clear that
k - 2 = 3
⇒ k = 5.
APPEARS IN
संबंधित प्रश्न
Draw the graph of the following linear equations in two variables:- 3 = 2x + y
If the point (2, -2) lies on the graph of the linear equation 5x + ky = 4, find the value of k.
Draw the graph of the equation given below. Also, find the coordinates of the point
where the graph cuts the coordinate axes : 6x − 3y = 12
Draw the graph of the equation given below. Also, find the coordinate of the points
where the graph cuts the coordinate axes : 3x + 2y + 6 = 0
Use the table given below to draw the graph.
| X | - 5 | - 1 | 3 | b | 13 |
| Y | - 2 | a | 2 | 5 | 7 |
From your graph, find the values of 'a' and 'b'.
State a linear relationship between the variables x and y.
Draw the graph (straight line) given by equation x - 3y = 18. If the straight line is drawn passes through the points (m, - 5) and (6, n); find the values of m and n.
Solve, graphically, the following pairs of equation :
x - 5 = 0
y + 4 = 0
Find the values.
y = 3x + 1
| x | − 1 | 0 | 1 | 2 |
| y |
The graph of the linear equation x + 2y = 7 passes through the point (0, 7).
The graph of every linear equation in two variables need not be a line.
