Advertisements
Advertisements
प्रश्न
Using the Remainder Theorem, factorise each of the following completely.
3x3 + 2x2 − 19x + 6
उत्तर
For x=2, the value of the given
expression `3x^3+2x^2-19x+6`
= `3(2)^3+2(2)^2-19(2)+6`
=`24+8-38+6`
= 0
⇒ x-2 is a factor of `3x^3+2x^2-19x+6`
Now let us do long division
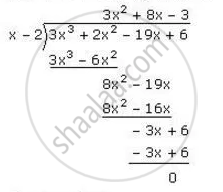
Thus we have ,
`3x^3+2x^2-19x+6` =`(x-2) (3x^2+8x-3) `
=`(x-2)(3x^2+9x-x-3)`
=`(x-2)(3x(x+3)-(x+3))`
= (x-2) (3x-1) (x+3)
APPEARS IN
संबंधित प्रश्न
Find the remainder when x3 + 3x2 + 3x + 1 is divided by x + π.
Use the Remainder Theorem to factorise the following expression:]
`2x^3 + x^2 - 13x + 6`
What number should be subtracted from x3 + 3x2 – 8x + 14 so that on dividing it by x – 2, the remainder is 10?
If (x – 2) is a factor of the expression 2x3 + ax2 + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b.
Using remainder theorem, find the remainder on dividing f(x) by (x + 3) where f(x) = 2x2 – 5x + 1
If on dividing 2x3 + 6x2 – (2k – 7)x + 5 by x + 3, the remainder is k – 1 then the value of k is
If x51 + 51 is divided by x + 1, then the remainder is
By Remainder Theorem find the remainder, when p(x) is divided by g(x), where p(x) = x3 – 2x2 – 4x – 1, g(x) = x + 1
Check whether p(x) is a multiple of g(x) or not:
p(x) = x3 – 5x2 + 4x – 3, g(x) = x – 2
The polynomial p(x) = x4 – 2x3 + 3x2 – ax + 3a – 7 when divided by x + 1 leaves the remainder 19. Find the values of a. Also find the remainder when p(x) is divided by x + 2.
