Advertisements
Advertisements
प्रश्न
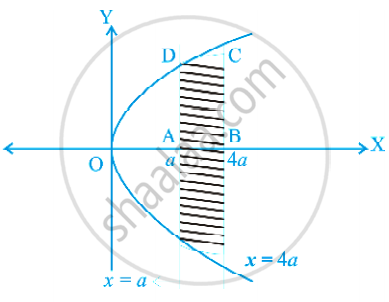
वक्र x = at2 और y = 2at द्वारा t = 1 और t = 2 के संगत कोटियों के बीच परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
उत्तर
दिया है : x = at2 ...(i),
y = 2at ...(ii)
जिससे t = `"y"/(2"a")` हुआ।
t का यह मान (i) में रखने पर,
हमें प्राप्त होता है : y2 = 4ax।
(i) में t = 1 और t = 2 रखने पर,
हमें x = a, और x = 4a प्राप्त होते हैं।
आकृति 8.7 से, वाँछित क्षेत्रफल
= 2 * ABCD का क्षेत्रफल
= `2 int_"a"^(4"a") "yd"x`
= `2 xx 2 int_"a"^(4"a") sqrt("a"x) "d"x`
= `8sqrt("a") |(x)^(3/2)/3|_"a"^(4"a")`
= `56/3 "a"^2` वर्ग इकाई
APPEARS IN
संबंधित प्रश्न
वक्र ay2 = x3, y-अक्ष तथा y = a और y = 2a रेखाओं द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

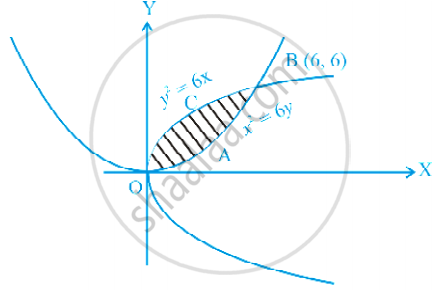
परवलयों y2 = 6x और x2 = 6y से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
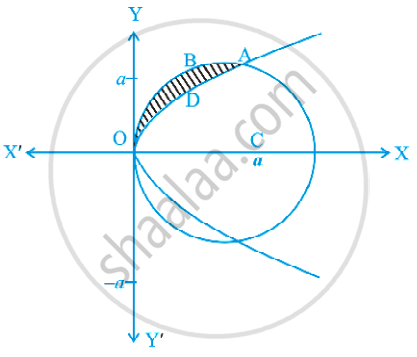
x-अक्ष के ऊपर परवलय y2 = ax और वृत्त x2 + y2 = 2ax के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
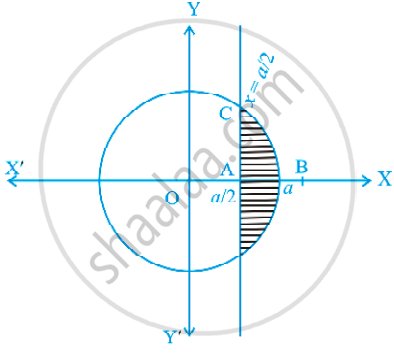
रेखा x = `"a"/2` द्वारा वृत्त x2 + y2 = a2 के काटे गए एक लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए।
वृत्त x2 + y2 = 2 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल बराबर है
दीर्घवृत्त `x^2/"a"^2 + y^2/"b"^2` = 1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल बराबर है
वक्र y = x2 और रेखा y = 16 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र y = x2 + x, x-अक्ष तथा x = 2 और x = 5 रेखाओं से परिबद्ध क्षेत्र का क्षेत्रफल के ______ बराबर है।
परवलय y2 = 2px, और x2 = 2py से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = x3 , y = x + 6 और x = 0 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
क्षेत्र `{(x, 0) : y = sqrt(4 - x^2)}` और x-अक्ष का चित्रण कीजिए। समाकलन का उपयोग करते हुए इस क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = 2`sqrtx` के अंतर्गत x = 0 और x = 1 रेखाओं के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = `sqrt("a"^2 - x^2)` के अंतर्गत तथा x = 0 और x = a रेखाओं के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y2 = 2x और x2 + y2 = 4x से परिंबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
रेखा x + 2y = 2, y – x = 1 और 2x + y = 7 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = 2cosx तथा x-अक्ष द्वारा x = 0 से x = 2π तक परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थाश में, x-अक्ष, रेखा y = x और वृत्त x2 + y2 = 32 द्वारा घिरे क्षेत्र का क्षेत्रफल है-
परवलय y2 = x और सरल रेखा 2y = x से परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र y = sinx द्वारा कोटि x = 0, और x = `pi/2` तथा x-अक्ष के बीच परिबद्ध क्षेत्र का क्षेत्रफल है
वृत्त x2 + y2 = 1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र x = 2y + 3 तथा y = 1 और y = –1 रेखाओं द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
