Advertisements
Advertisements
प्रश्न
वक्रों y = x एवं y = x2 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
उत्तर
वक्रों के समी० y = x …(i)
y = x2 ….(ii)
समीकरण (i) एक सीधी रेखा को प्रदर्शित करता है जो मूल बिन्दु से गुजरती है तथा समीकरण (ii) एक परवलय को प्रदर्शित करती है जिसका शीर्ष (0, 0) है।
समीकरण (i) व (ii) को परस्पर हल करने पर प्रतिच्छेदन बिन्दु (0, 0) और (1, 1) प्राप्त होते हैं।
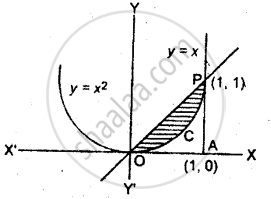
अभीष्ट क्षेत्रफल = OCPO का क्षेत्रफल
`= int_0^1 ("y"_2 - "y"_1) "dx"`
`= int_0^1 (x - x^2) "dx"` जहाँ y2 = x, y1 = x2
`= [x^2/2 - x^3/3]_0^1`
`= [1/2 - 1/3] - 0`
`= 1/6` वर्ग इकाई
APPEARS IN
संबंधित प्रश्न
परवलय x2 = 4y और वृत्त 4x2 + 4y2 = 9 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्रों (x - 1)2 + y = 1 एवं x2 + y2 = 1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्रों y = x2 + 2, y = x, x = 0 एवं x = 3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समाकलन का उपयोग करते हुए एक ऐसे त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (-1, 0), (1, 3) एवं (3, 2) हैं।
समाकलन का उपयोग करते हुए एक ऐसे त्रिकोणीय क्षेत्र का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओं के समीकरण y = 2x + 1, y = 3x + 1 एवं x = 4 हैं।
वृत्त x2 + y2 = 4 एवं रेखा x + y = 2 से घिरे छोटे भाग का क्षेत्रफल है:
वक्रों y2 = 4x एवं y = 2x के मध्यवर्ती क्षेत्र का क्षेत्रफल है:
y = |x + 3| का ग्राफ खींचिए एवं `int_(- 6)^0 |x + 3| dx` का मान ज्ञात कीजिए।
