Advertisements
Advertisements
प्रश्न
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/hr. How much area will it irrigate in 10 minutes if 8 cm of standing water is needed for irrigation?
उत्तर
We have,
Width of the canal, b = 6 m
Depth of the canal, h = 1.5 m,
Height of the standing water needed for irrigation, H=8 cm = 0.08 m,
speed of the flowing water, l=4 km / h `= 4000/60 = 200/3 "m"// "min"`
Now,
Volume of water flowing out from canal in 1 min =lbh
`=200/3xx6xx1.5`
=600 m2
⇒ Volume of water flowing out from canal in 10 min = 600 × 10 = 6000 m3
`"so, the area of irrigation" = "Volume of water flowing out from canal in 10 min"/"Height of the standing water needed for irrigation"`
`= 6000/0.08`
= 75000 m2
= 7.5 hectare (As, 1 hectare = 10000 m2)
Hence, it will irrigate 7.5 hectare of area in 10 minutes.
APPEARS IN
संबंधित प्रश्न
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand. If the height of this conical heap is 24 cm, then find its slant height correct upto one place of decimal?
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use \[\pi = \frac{22}{7}\]]
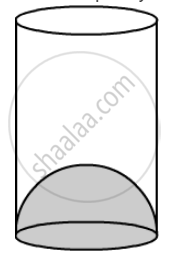
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
Three cubes of iron whose edges are 6 cm, 8 cm and 10 cm, respectively are melted and formed into a single cube. Find the edge of the new cube formed.
The curved surface area of a sphere is 5544 cm2. Find its volume.
Choose the correct answer of the following question:
The surface areas of two spheres are in the ratio 16 : 9. The ratio of their volumes is
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
The slant height of a bucket is 26 cm. The diameter of upper and lower circular ends are 36 cm and 16 cm. then height of bucket is ______.
Match the column:
| (1) surface area of cuboid | (A) πr2h |
| (2) surface area of closed right cylinder | (B) 2πr(h + r) |
| (3) Total surface area of right cone | (C) πrl + πr2 |
| (4) Total surface area of hemisphere | (D) 3πr3 |
| (E) 3πr2 | |
| (F) 2[lb + bh + lh] |
The radius of a metal sphere is 3 cm. The sphere is melted and made into a long wire of uniform circular cross-section, whose length is 36 cm. To calculate the radius of wire, complete the following activity.
Radius of the sphere = `square`
Length of the wire = `square`
Let the radius of the wire by r cm.
Now, Volume of the wire = Volume of the `square`
`square` = `square`
r2 × `square` = `square` × `square`
r2 × `square` = `square`
r = `square`
Hence, the radius of the wire is `square` cm.
