Advertisements
Advertisements
प्रश्न
Write the zeros of the polynomial x2 − x − 6.
उत्तर
We have to find the zeros of the polynomial `x ^2 - x-6`
`f(x)= x^2 - x-6`
`f(x)= x^2 - 3x + 2x -6`
`f(x) = x(x-3)+2 (x-3)`
`f(x) = (x + 2) (x - 3)`
We know that if `(x - a)` is a factor of f(x) then x = a is a zero of polynomial
Therefore we have
`x + 2 = 0`
` x = -2`
Also
` x - 3 = 0 `
`x = 3 `
Hence, the zeros of polynomial `x^2 - x- 6` is ` 3 , -2`
APPEARS IN
संबंधित प्रश्न
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials
`7t^4+4t^3+3t-2`
Write the standard form of a linear polynomial with real coefficients.
The graph of a polynomial y = f(x), shown in Fig. 2.18. Find the number of real zeros of f(x).
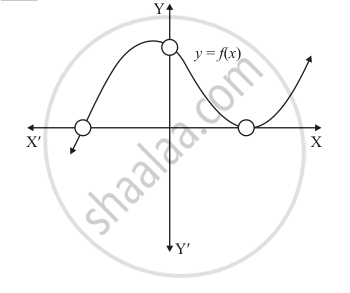
The graph of the polynomial f(x) = ax2 + bx + c is as shown in Fig. 2.20. Write the value of b2 − 4ac and the number of real zeros of f(x).

If f(x) = x3 + x2 − ax + b is divisible by x2 − x write the value of a and b.
If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f(x)?
If α, β are the zeros of polynomial f(x) = x2 − p (x + 1) − c, then (α + 1) (β + 1) =
Figure 2.23 show the graph of the polynomial f(x) = ax2 + bx + c for which

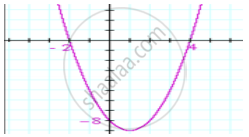
An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.


In the graph, how many zeroes are there for the polynomial?
Classify the following as a constant, linear, quadratic and cubic polynomials:
`sqrt(2)x - 1`
