ISC (Arts) कक्षा १२ - CISCE Important Questions for Mathematics

Let f : W → W be defined as

`f(n)={(n-1, " if n is odd"),(n+1, "if n is even") :}`

Show that f is invertible a nd find the inverse of f. Here, W is the set of all whole
numbers.

The binary operation *: R x R → R is defined as a *b = 2a + b Find (2 * 3)*4

Solve `3tan^(-1)x + cot^(-1) x = pi`

If the function `f(x) = sqrt(2x - 3)` is invertible then find its inverse. Hence prove that `(fof^(-1))(x) = x`

if `tan^(-1) a + tan^(-1) b + tan^(-1) x = pi`, prove that a + b + c = abc 

Let \[f\left(x\right) = x^3\] be a function with domain {0, 1, 2, 3}. Then domain of \[f^{-1}\] is ______.

Solve:  sin(2 tan ^-1 x)=1

If f A→ A and A=R - `{8/5}` , show that the function `f (x) = (8x + 3)/(5x - 8)` is one-one onto. Hence,find `f^-1`.

Solve for x:
`tan^-1 [(x-1),(x-2)] + tan^-1 [(x+1),(x+2)] = x/4`

if sec^-1  x = cosec^-1  v. show that `1/x^2 + 1/y^2 = 1`

 Evaluate: `int_-6^3 |x+3|dx`

Solve for x, if:

tan (cos^-1x) = `2/sqrt5`

Prove that the line 2x - 3y = 9 touches the conics y² = -8x. Also, find the point of contact.

If A, B and C are the elements of Boolean algebra, simplify the expression (A’ + B’) (A + C’) + B’ (B + C). Draw the simplified circuit.

Prove that locus of z is circle and find its centre and radius if is purely imaginary.

If `sin^-1"x" + tan^-1"x" = pi/2`, prove that `2"x"^2 + 1 = sqrt5`  

Write the Boolean function corresponding to the switching circuit given below:

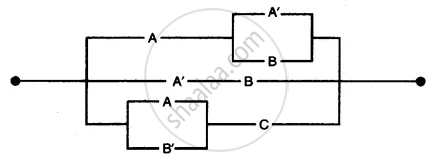
A, B and C represent switches in ‘on’ position and A’, B’ and C’ represent them in ‘off position. Using Boolean algebra, simplify the function and construct an equivalent switching circuit.

A relation R on (1, 2, 3) is given by R = {(1, 1), (2, 2), (1, 2), (3, 3), (2, 3)}. Then the relation R is ______.

If f(x) = [4 – (x – 7)³]^1/5 is a real invertible function, then find f^–1(x).

Let A = R – {2} and B = R – {1}. If f: A `→` B is a function defined by f(x) = `(x - 1)/(x - 2)` then show that f is a one-one and an onto function.