Advertisements
Advertisements
Using encoding matrix `[(1,1),(0,1)]`encode and decode the message
“ALL IS WELL” .
Concept: Application of Inverse of a Matrix to Coding Theory
Show that the following equations: -2x + y + z = a, x - 2y + z = b, x + y - 2z = c have no solutions unless a +b + c = 0 in which case they have infinitely many solutions. Find these solutions when a=1, b=1, c=-2.
Concept: Rank of a Matrix Using Echelon Forms
Find non singular matrices P and Q such that A = `[(1,2,3,2),(2,3,5,1),(1,3,4,5)]`
Concept: PAQ in normal form
Show that a matrix A = `1/2[(sqrt2,-isqrt2,0),(isqrt2,-sqrt2,0),(0,0,2)]` is unitary.
Concept: Types of Matrices
If 𝒙 = r cos θ and y= r sin θ prove that JJ-1=1.
Concept: Types of Matrices
Using coding matrix A=`[(2,1),(3,1)]` encode the message THE CROW FLIES AT MIDNIGHT.
Concept: Types of Matrices
Find the non-singular matrices P & Q such that PAQ is in normal form where`[(1,2,3,4),(2,1,4,3),(3,0,5,-10)]`
Concept: Types of Matrices
Investigate for what values of λ and μ the equations
2x + 3y + 5z = 9
7x + 3y - 2z = 8
2x + 3y + λz = μ have
A. No solutions
B. Unique solutions
C. An infinite number of solutions.
Concept: Types of Matrices
Find the maximum and minimum values of `f(x,y)=x^3+3xy^2-15x^2-15y^2+72x`
Concept: Total Differentials
If x = u+v+w, y = uv+vw+uw, z = uvw and φ is a function of x, y and z
Prove that 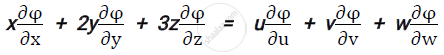
Concept: Euler’s Theorem on Homogeneous functions with two and three independent variables (with proof)
If tan(θ+iφ)=tanα+isecα
Prove that
1)`e^(2varphi)=cot(varphi/2)`
2) `2theta=npi+pi/2+alpha`
Concept: Euler’s Theorem on Homogeneous functions with two and three independent variables (with proof)
If `z=tan(y-ax)+(y-ax)^(3/2)` then show that `(del^2z)/(delx^2)= a^2 (del^2z)/(dely^2)`
Concept: Partial Derivatives of First and Higher Order
State Euler’s theorem on homogeneous function of two variables and if `u=(x+y)/(x^2+y^2)` then evaluate `x(delu)/(delx)+y(delu)/(dely`
Concept: Euler’s Theorem on Homogeneous functions with two and three independent variables (with proof)
If u =`f((y-x)/(xy),(z-x)/(xz)),` show that `x^2(delu)/(delx)+y^2(delu)/(dely)+z^2(delu)/(delz)=0`.
Concept: Euler’s Theorem on Homogeneous functions with two and three independent variables (with proof)
If `u=sin^(-1)((x+y)/(sqrtx+sqrty))`,Prove that
`x^2u_(x x)+2xyu_(xy)+y^2u_(yy)=(-sinu.cos2u)/(4cos^3u)`
Concept: Euler’s Theorem on Homogeneous functions with two and three independent variables (with proof)
State and Prove Euler’s Theorem for three variables.
Concept: Euler’s Theorem on Homogeneous functions with two and three independent variables (with proof)
If `u=e^(xyz)f((xy)/z)` where `f((xy)/z)` is an arbitrary function of `(xy)/z.`
Prove that: `x(delu)/(delx)+z(delu)/(delz)=y(delu)/(dely)+z(delu)/(delz)=2xyz.u`
Concept: Partial Derivatives of First and Higher Order
If Z=f(x.y). x=r cos θ, y=r sinθ. prove that `((delz)/(delx))^2+((delz)/(dely))^2=((delz)/(delr))^2+1/r^2((delz)/(delθ))^2`
Concept: Differentiation of Implicit Functions
State and prove Euler’s Theorem for three variables.
Concept: Euler’s Theorem on Homogeneous functions with two and three independent variables (with proof)
If z = f (x, y) where x = eu +e-v, y = e-u - ev then prove that `(delz)/(delu)-(delz)/(delv)=x(delz)/(delx)-y(delz)/(dely).`
Concept: Euler’s Theorem on Homogeneous functions with two and three independent variables (with proof)
