Topics
Linear equations in two variables
- Introduction to linear equations in two variables
- Methods of solving linear equations in two variables
- Simultaneous method
- Simultaneous method
- Substitution Method
- Cross - Multiplication Method
- Graphical Method
- Determinant method
- Determinant of Order Two
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Simple Situational Problems
- Pair of Linear Equations in Two Variables
- Application of simultaneous equations
- Simultaneous method
Quadratic Equations
- Quadratic Equations
- Roots of a Quadratic Equation
- Solutions of Quadratic Equations by Factorization
- Solutions of Quadratic Equations by Completing the Square
- Formula for Solving a Quadratic Equation
- Nature of Roots of a Quadratic Equation
- The Relation Between Roots of the Quadratic Equation and Coefficients
- To Obtain a Quadratic Equation Having Given Roots
- Application of Quadratic Equation
Arithmetic Progression
- Introduction to Sequence
- Terms in a sequence
- Arithmetic Progression
- General Term of an Arithmetic Progression
- Sum of First ‘n’ Terms of an Arithmetic Progressions
- Arithmetic Progressions Examples and Solutions
- Geometric Progression
- General Term of an Geomatric Progression
- Sum of the First 'N' Terms of an Geometric Progression
- Geometric Mean
- Arithmetic Mean - Raw Data
- Concept of Ratio
Financial Planning
Probability
- Probability - A Theoretical Approach
- Basic Ideas of Probability
- Random Experiments
- Outcome
- Equally Likely Outcomes
- Sample Space
- Event and Its Types
- Probability of an Event
- Type of Event - Elementry
- Type of Event - Complementry
- Type of Event - Exclusive
- Type of Event - Exhaustive
- Concept Or Properties of Probability
- Addition Theorem
Statistics
- Tabulation of Data
- Inclusive and Exclusive Type of Tables
- Ogives (Cumulative Frequency Graphs)
- Applications of Ogives in Determination of Median
- Relation Between Measures of Central Tendency
- Introduction to Normal Distribution
- Properties of Normal Distribution
- Concepts of Statistics
- Mean of Grouped Data
- Method of Finding Mean for Grouped Data: Direct Method
- Method of Finding Mean for Grouped Data: Deviation Or Assumed Mean Method
- Method of Finding Mean for Grouped Data: the Step Deviation Method
- Median of Grouped Data
- Mode of Grouped Data
- Concept of Pictograph
- Presentation of Data
- Graphical Representation of Data as Histograms
- Frequency Polygon
- Concept of Pie Graph (Or a Circle-graph)
- Interpretation of Pie Diagram
- Drawing a Pie Graph
Concept of Pictograph
A pictograph is the representation of data using pictures. Pictographs represent the frequency of data using symbols or images that are relevant to the data.
This is one of the simplest ways to represent data.
- Pictographs were used as the earliest known form of writing, with examples having been discovered in Egypt and Mesopotamia since 3000 BC.
- A pictograph is also called a Pictogram.
- The data can be easily analysed and interpreted.
For example:
The modes of travelling to school by 160 students are given below:
| Mode | By walking | On bicycle | By car | By bus |
| No. of students | 30 | 50 | 20 | 60 |
Draw a suitable pictograph.
Solution :
Since every given number of data is completely divisible by 10, therefore the scale will be:

The required pictograph will be as shown below :
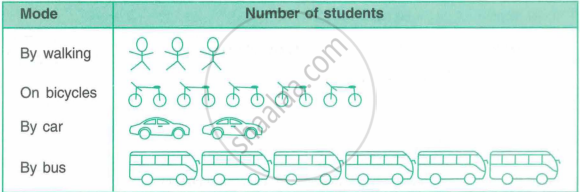
Shaalaa.com | What Is Pictograph
Related QuestionsVIEW ALL [30]
Mr. Dinesh collected the information about the rainfall of a particular city in a week from the newspaper and recorded his information in the pictograph.
| Millimeters of Rain | |
| Sunday |  |
| Monday |  |
| Tuesday |  |
| Wednesday |  |
| Thursday |  |
| Friday |  |
| Saturday |  |

a. On which day, the rain was most?
b. On which day, the rain was least?
c. How much rain was there on Sunday?
d. How much rain was there on Monday?
e. Find total rainfall of the city in that week?
The following pictograph shows the number of cars sold by four dealers A, B, C and D in a city. Scale:  = 50 cars.
= 50 cars.
| Dealer | Number of cars |
| A |    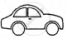 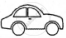 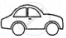 |
| B | 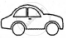  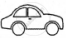 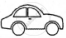  |
| C | 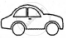 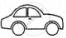 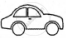 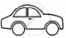 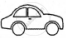 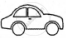 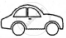 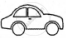 |
| D | 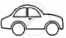 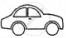   |
Using the pictograph, drawn above, answer the following questions:
What is the total number of cars sold by all the dealers?
A survey was carried out in a certain school to find out the popular school subjects among students of Classes VI to VIII. The data in this regard is displayed as pictograph given below:
| Subject | Number of Students |
| Hindi | |
| English | |
| Mathematics | |
| Science | |
| Social Studies |
(a) Which subject is most popular among the students?
(b) How many students like Mathematics?
(c) Find the number of students who like subjects other than Mathematics and Science.
The following pictograph shows the number of cars sold by four dealers A, B, C and D in a city. Scale:  = 50 cars.
= 50 cars.
| Dealer | Number of cars |
| A |       |
| B |      |
| C |         |
| D |     |
Using the pictograph, drawn above, answer the following questions:
How many more cars have dealer A sold as compared to dealer D?
The number of bottles of cold drinks sold by a shopkeeper on six consecutive days is as follows:
| Day | Sunday | Monday | Tuesday | Wednesday | Thursday | Friday |
| Number of bottles | 350 | 200 | 300 | 250 | 100 | 150 |
Prepare a pictograph of the data using one symbol to represent 50 bottles.
The following pictograph shows the number of watches manufactured by a factory, in a particular weeks.
| Day | Number of watches |
| Monday |         |
| Tuesday |            |
| Wednesday |       |
| Thursday |       |
| Friday |      |
| Saturday |         |
Scale:  = 100 watches
= 100 watches
Find the total number of watches manufactured in the whole week?
Annual expenditure of a company in the year 2007-2008 is given below:
| Items | Expenditure (Rs in lakh) |
| Salaries of employees | 65 |
| Advertisement | 10 |
| Purchase of machiner | 85 |
| Electricity and water | 15 |
| Transportation | 25 |
| Other expenses | 30 |
Prepare a pictograph of the above data using an appropriate symbol to represent Rs 10 lakh.
The following pictograph shows the number of watches manufactured by a factory, in a particular weeks.
| Day | Number of watches |
| Monday |         |
| Tuesday |            |
| Wednesday |       |
| Thursday |       |
| Friday |      |
| Saturday |         |
Scale:  = 100 watches
= 100 watches
Find on which day was the least number of watches manufactured?
