Topics
Physical World and Measurement
Physical World
Units and Measurements
- International System of Units
- Measurement of Length
- Measurement of Mass
- Measurement of Time
- Accuracy, Precision and Least Count of Measuring Instruments
- Errors in Measurements
- Significant Figures
- Dimensions of Physical Quantities
- Dimensional Formulae and Dimensional Equations
- Dimensional Analysis and Its Applications
- Need for Measurement
- Units of Measurement
- Fundamental and Derived Units
- Length, Mass and Time Measurements
- Introduction of Units and Measurements
Motion in a Straight Line
- Position, Path Length and Displacement
- Average Velocity and Average Speed
- Instantaneous Velocity and Speed
- Kinematic Equations for Uniformly Accelerated Motion
- Acceleration (Average and Instantaneous)
- Relative Velocity
- Elementary Concept of Differentiation and Integration for Describing Motion
- Uniform and Non-uniform Motion
- Uniformly Accelerated Motion
- Position-time, Velocity-time and Acceleration-time Graphs
- Position - Time Graph
- Relations for Uniformly Accelerated Motion (Graphical Treatment)
- Introduction of Motion in One Dimension
- Motion in a Straight Line
Kinematics
Motion in a Plane
- Scalars and Vectors
- Multiplication of Vectors by a Real Number or Scalar
- Addition and Subtraction of Vectors - Graphical Method
- Resolution of Vectors
- Vector Addition – Analytical Method
- Motion in a Plane
- Motion in a Plane with Constant Acceleration
- Projectile Motion
- Uniform Circular Motion (UCM)
- General Vectors and Their Notations
- Motion in a Plane - Average Velocity and Instantaneous Velocity
- Rectangular Components
- Scalar (Dot) and Vector (Cross) Product of Vectors
- Relative Velocity in Two Dimensions
- Cases of Uniform Velocity
- Cases of Uniform Acceleration Projectile Motion
- Motion in a Plane - Average Acceleration and Instantaneous Acceleration
- Angular Velocity
- Introduction of Motion in One Dimension
Laws of Motion
Work, Energy and Power
Laws of Motion
- Aristotle’s Fallacy
- The Law of Inertia
- Newton's First Law of Motion
- Newton’s Second Law of Motion
- Newton's Third Law of Motion
- Conservation of Momentum
- Equilibrium of a Particle
- Common Forces in Mechanics
- Circular Motion and Its Characteristics
- Solving Problems in Mechanics
- Static and Kinetic Friction
- Laws of Friction
- Inertia
- Intuitive Concept of Force
- Dynamics of Uniform Circular Motion - Centripetal Force
- Examples of Circular Motion (Vehicle on a Level Circular Road, Vehicle on a Banked Road)
- Lubrication - (Laws of Motion)
- Law of Conservation of Linear Momentum and Its Applications
- Rolling Friction
- Introduction of Motion in One Dimension
Work, Energy and Power
- Introduction of Work, Energy and Power
- Notions of Work and Kinetic Energy: the Work-energy Theorem
- Kinetic Energy (K)
- Work Done by a Constant Force and a Variable Force
- Concept of Work
- Potential Energy (U)
- Conservation of Mechanical Energy
- Potential Energy of a Spring
- Various Forms of Energy : the Law of Conservation of Energy
- Power
- Collisions
- Non - Conservative Forces - Motion in a Vertical Circle
Motion of System of Particles and Rigid Body
System of Particles and Rotational Motion
- Motion - Rigid Body
- Centre of Mass
- Motion of Centre of Mass
- Linear Momentum of a System of Particles
- Vector Product of Two Vectors
- Angular Velocity and Its Relation with Linear Velocity
- Torque and Angular Momentum
- Equilibrium of Rigid Body
- Moment of Inertia
- Theorems of Perpendicular and Parallel Axes
- Kinematics of Rotational Motion About a Fixed Axis
- Dynamics of Rotational Motion About a Fixed Axis
- Angular Momentum in Case of Rotation About a Fixed Axis
- Rolling Motion
- Momentum Conservation and Centre of Mass Motion
- Centre of Mass of a Rigid Body
- Centre of Mass of a Uniform Rod
- Rigid Body Rotation
- Equations of Rotational Motion
- Comparison of Linear and Rotational Motions
- Values of Moments of Inertia for Simple Geometrical Objects (No Derivation)
Gravitation
Gravitation
- Kepler’s Laws
- Newton’s Universal Law of Gravitation
- The Gravitational Constant
- Acceleration Due to Gravity of the Earth
- Acceleration Due to Gravity Below and Above the Earth's Surface
- Acceleration Due to Gravity and Its Variation with Altitude and Depth
- Gravitational Potential Energy
- Escape Speed
- Earth Satellites
- Energy of an Orbiting Satellite
- Geostationary and Polar Satellites
- Weightlessness
- Escape Velocity
- Orbital Velocity of a Satellite
Properties of Bulk Matter
Mechanical Properties of Solids
- Elastic Behaviour of Solid
- Stress and Strain
- Hooke’s Law
- Stress-strain Curve
- Young’s Modulus
- Determination of Young’s Modulus of the Material of a Wire
- Shear Modulus or Modulus of Rigidity
- Bulk Modulus
- Application of Elastic Behaviour of Materials
- Elastic Energy
- Poisson’s Ratio
Thermodynamics
Behaviour of Perfect Gases and Kinetic Theory of Gases
Mechanical Properties of Fluids
- Thrust and Pressure
- Pascal’s Law
- Variation of Pressure with Depth
- Atmospheric Pressure and Gauge Pressure
- Hydraulic Machines
- Streamline and Turbulent Flow
- Applications of Bernoulli’s Equation
- Viscous Force or Viscosity
- Reynold's Number
- Surface Tension
- Effect of Gravity on Fluid Pressure
- Terminal Velocity
- Critical Velocity
- Excess of Pressure Across a Curved Surface
- Introduction of Mechanical Properties of Fluids
- Archimedes' Principle
- Stoke's Law
- Equation of Continuity
- Torricelli's Law
Oscillations and Waves
Thermal Properties of Matter
- Heat and Temperature
- Measurement of Temperature
- Ideal-gas Equation and Absolute Temperature
- Thermal Expansion
- Specific Heat Capacity
- Calorimetry
- Change of State - Latent Heat Capacity
- Conduction
- Convection
- Radiation
- Newton’s Law of Cooling
- Qualitative Ideas of Black Body Radiation
- Wien's Displacement Law
- Stefan's Law
- Anomalous Expansion of Water
- Liquids and Gases
- Thermal Expansion of Solids
- Green House Effect
Thermodynamics
- Thermal Equilibrium
- Zeroth Law of Thermodynamics
- Heat, Internal Energy and Work
- First Law of Thermodynamics
- Specific Heat Capacity
- Thermodynamic State Variables and Equation of State
- Thermodynamic Process
- Heat Engine
- Refrigerators and Heat Pumps
- Second Law of Thermodynamics
- Reversible and Irreversible Processes
- Carnot Engine
Kinetic Theory
- Molecular Nature of Matter
- Gases and Its Characteristics
- Equation of State of a Perfect Gas
- Work Done in Compressing a Gas
- Introduction of Kinetic Theory of an Ideal Gas
- Interpretation of Temperature in Kinetic Theory
- Law of Equipartition of Energy
- Specific Heat Capacities - Gases
- Mean Free Path
- Kinetic Theory of Gases - Concept of Pressure
- Assumptions of Kinetic Theory of Gases
- RMS Speed of Gas Molecules
- Degrees of Freedom
- Avogadro's Number
Oscillations
- Periodic and Oscillatory Motion
- Simple Harmonic Motion (S.H.M.)
- Simple Harmonic Motion and Uniform Circular Motion
- Velocity and Acceleration in Simple Harmonic Motion
- Force Law for Simple Harmonic Motion
- Energy in Simple Harmonic Motion
- Some Systems Executing Simple Harmonic Motion
- Damped Simple Harmonic Motion
- Forced Oscillations and Resonance
- Displacement as a Function of Time
- Periodic Functions
- Oscillations - Frequency
- Simple Pendulum
Waves
- Reflection of Transverse and Longitudinal Waves
- Displacement Relation for a Progressive Wave
- The Speed of a Travelling Wave
- Principle of Superposition of Waves
- Introduction of Reflection of Waves
- Standing Waves and Normal Modes
- Beats
- Doppler Effect
- Wave Motion
- Speed of Wave Motion
- Scalars
- Vectors
- Position vector
- Displacement vector
- Resultant vector
Notes
Scalars and Vectors
Mathematics and Science were invented by humans to understand and describe the world around us. A lot of mathematical quantities are used in Physics to explain the concepts clearly. A few examples of these include force, speed, velocity and work. These quantities are often described as being a scalar or a vector quantity. Scalars and vectors are differentiated depending on their definition.
A scalar quantity is defined as the physical quantity that has only magnitude, for example, length, speed, work, mass, density, etc.
On the other hand, a vector quantity is defined as the physical quantity that has both, magnitude as well as direction like displacement, force, torque, momentum, acceleration, velocity, etc.
The other way of differentiating these two quantities is by using a notation. 
Characteristics of Vectors
-
These possess both magnitude and direction.
-
These do not obey the ordinary law of algebra.
-
These change if either magnitude or direction or both change.
- These are represented by bold-faced letters having arrow over them.
Equality of Vectors
Two vectors A and B are said to be equal if, and only if, they have the same magnitude and the same direction. Figure below shows two equal vectors A and B. We can easily check their equality. Shift B parallel to itself until its tail Q coincides with that of A, i.e. Q coincides with O. Then, since their tips S and P also coincide, the two vectors are said to be equal. In general, equality is indicated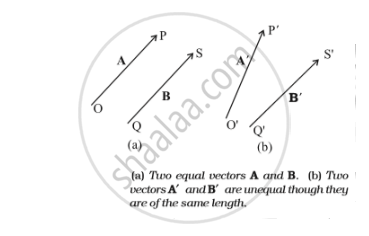
as A = B. Note that in Fig.(b) above, vectors A′ and B′ have the same magnitude but they are not equal because they have different directions. Even if we shift B′ parallel to itself so that its tail Q′ coincides with the tail O′ of A′ , the tip S′ of B′ does not coincide with the tip P′ of A′ .
Position And Displacement Vectors
One of the primary things to start with Kinematics is to know what position vector is, what displacement vector is, and what the difference between position vector and displacement vector is.
Position Vector:
Position vector is used to specify the position of a certain body. Knowing the position of a body is vital when it comes to describe the motion of that body. The position vector of an object is measured from the origin, in general. Suppose an object is placed in the space as shown below: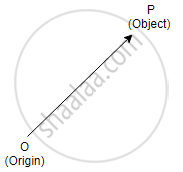
Position vector`(bar r)=xî+ yhat j + zhat k`
Where,
î = unit vector along x direction
`hat j` = unit vector along y direction
`hat k` = unit vector along z direction
So if an object is at a certain point P (say) at a certain time, its position vector is given as described above.
Displacement Vector:
The displacement vector is a vector which gives the position of a point with reference to a point other than the origin of the co-ordinate system.
The change in the position vector of an object is known as displacement vector. Suppose an object is at point A at time = 0 and at point B at time = t. The position vectors of the object at point A and at point B are given as:
Position vector at A =`hat r_A=5hat i+3 hat j + 4 hat k`
Position vector at B =`hat r_B=2 hat i+2 hat j + 1 hat k`
Now, the displacement vector of the object from time interval 0 to t will be:
`hat r_B - hat r_A= -3 hat i - hat j - 3 hat k`
The displacement of an object can also be defined as the vector distance between the initial point and the final point. Suppose an object travels from point A to point B in the path shown in the black curve below
The displacement of the particle would be the vector line AB, headed in the direction A to B. The direction of displacement vector is always headed from initial point to the final point.
Shaalaa.com | Motion in plane part 1 (Introduction to Scalar and Vector)
Series: 1
00:10:32 undefined
00:03:57 undefined
00:11:14 undefined
00:13:59 undefined
00:10:50 undefined
00:03:55 undefined
00:07:23 undefined
00:06:12 undefined
