Advertisements
Advertisements
प्रश्न
A body of mass M is kept on a rough horizontal surface (friction coefficient = μ). A person is trying to pull the body by applying a horizontal force but the body is not moving. The force by the surface on A is F, where
पर्याय
F = Mg
F = μ Mg
Mg ≤ F ≤ Mga `sqrt(1+mu^2)`
Mg ≥ F ≥ Mg `sqrt(1-mu^2)`
उत्तर
Mg ≤ F ≤ Mga `sqrt(1+mu^2)`
Let T be the force applied on an object of mass M.
If T = 0, Fmin = Mg.
If T is acting in the horizontal direction, then the body is not moving.
∴ T = μ(mg)
Fmax = `sqrt("Mg"^2+"T"^2)`
= `sqrt("Mg"^2+(mu"Mg")^2)`
Thus, we have:
Mg ≤ F ≤ Mga `sqrt(1+mu^2)`
APPEARS IN
संबंधित प्रश्न
A boy of mass M is applying a horizontal force to slide a box of mass M' on a rough horizontal surface. The coefficient of friction between the shoes of the boy and the floor is μ and that between the box and the floor is μ'. In which of the following cases it is certainly not possible to slide the box?
Mark the correct statements about the friction between two bodies.
(a) Static friction is always greater than the kinetic friction.
(b) Coefficient of static friction is always greater than the coefficient of kinetic friction.
(c) Limiting friction is always greater than the kinetic friction.
(d) Limiting friction is never less than static friction.
A block is placed on a rough floor and a horizontal force F is applied on it. The force of friction f by the floor on the block is measured for different values of F and a graph is plotted between them.
(a) The graph is a straight line of slope 45°.
(b) The graph is a straight line parallel to the F-axis.
(c) The graph is a straight line of slope 45° for small F and a straight line parallel to the F-axis for large F.
(d) There is a small kink on the graph.
A body slipping on a rough horizontal plane moves with a deceleration of 4.0 m/s2. What is the coefficient of kinetic friction between the block and the plane?
A block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest?
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ, find the frictional force acting on the block.
Repeat part (a) of problem 6 if the push is applied horizontally and not parallel to the incline.
In a children-park an inclined plane is constructed with an angle of incline 45° in the middle part (in the following figure). Find the acceleration of boy sliding on it if the friction coefficient between the cloth of the boy and the incline is 0.6 and g = 19 m/s2.

The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that, if λ be the angle of friction and μ the coefficient of static friction λ ≤ tan−1 μ.
In the following figure shows two blocks in contact sliding down an inclined surface of inclination 30°. The friction coefficient between the block of mass 2.0 kg and the incline is μ1, and that between the block of mass 4.0 kg and incline is μ2. Calculate the acceleration of the 2.0 kg block if (a) μ1 = 0.20 and μ2 = 0.30, (b) μ1 = 0.30 and μ2 = 0.20. Take g = 10 m/s2.
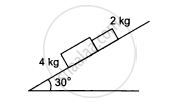
Two masses M1 and M2 are connected by a light rod and the system is slipping down a rough incline of angle θ with the horizontal. The friction coefficient at both the contacts is μ. Find the acceleration of the system and the force by the rod on one of the blocks.
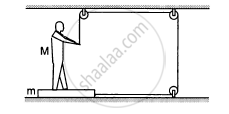
The friction coefficient between the board and the floor shown in the following figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.
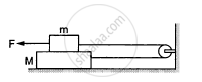
The friction coefficient between the two blocks shown in the following figure is μ but the floor is smooth. (a) What maximum horizontal force F can be applied without disturbing the equilibrium of the system? (b) Suppose the horizontal force applied is double of that found in part (a). Find the accelerations of the two masses.
Suppose the entire system of the previous questions is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
A block of mass m slips on a rough horizontal table under the action of a horizontal force applied to it. The coefficient of friction between the block and the table is μ. The table does not move on the floor. Find the total frictional force applied by the floor on the legs of the table. Do you need the friction coefficient between the table and the floor or the mass of the table?
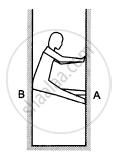
A person (40 kg) is managing to be at rest between two vertical walls by pressing one wall A by his hands and feet and the other wall B by his back (in the following figure). Assume that the friction coefficient between his body and the walls is 0.8 and that limiting friction acts at all the contacts. (a) Show that the person pushes the two wall with equal force. (b) Find the normal force exerted by either wall on the person. Take g = 10 m/s2.
The coefficient of static friction between a wooden block of mass 0.5 kg and a vertical rough wall is 0.2. The magnitude of horizontal force that should be applied on the block to keep it adhered to the wall will be ______ N. [g = 10 ms-2]
An inclined plane is bent in such a way that the vertical cross-section is given by Y = `x^2/4` where y is in vertical and x in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction µ = 0.5, the maximum height in cm at which a stationary block will not slip downward is ______ cm.
