Advertisements
Advertisements
प्रश्न
A cell of emf E is connected across an external resistance R. When current 'I' is drawn from the cell, the potential difference across the electrodes of the cell drops to V. The internal resistance 'r' of the cell is ______.
पर्याय
`((E - V)/E)R`
`((E - V)/R)`
`((E - V)R)/I`
`((E - V)/V)R`
उत्तर
A cell of emf E is connected across an external resistance R. When current 'I' is drawn from the cell, the potential difference across the electrodes of the cell drops to V. The internal resistance 'r' of the cell is `underlinebb(((E - V)/V)R)`.
Explanation:
The electromotive force (e) or e.m.f. is the energy provided by a cell or battery per coulomb of charge passing through it. It is measured in volts (V). It is equal to the potential difference across the terminals of the cell when no current is flowing through it. E = I(R + r), where E = electromotive force in volts, I = current in amperes, R = resistance of the load in the circuit in ohms, and r = internal resistance of the cell in ohms. That is, E = IR + Ir, E = V + Ir.
Rearranging the equation we get,
r = `((E - V))/I`
Substituting `I = V/R` in the above equation, we get,
r = `((E - V)R)/V`
∴ Internal resistance, r = `((E - V)R)/V`
संबंधित प्रश्न
Two cells of emfs 1.5 V and 2.0 V, having internal resistances 0.2 Ω and 0.3 Ω, respectively, are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance?
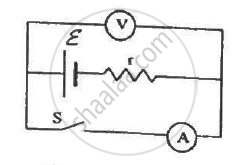
The following figure shows an arrangement to measure the emf ε and internal resistance r of a battery. The voltmeter has a very high resistance and the ammeter also has some resistance. The voltmeter reads 1.52 V when the switch S is open. When the switch is closed, the voltmeter reading drops to 1.45 V and the ammeter reads 1.0 A. Find the emf and the internal resistance of the battery.
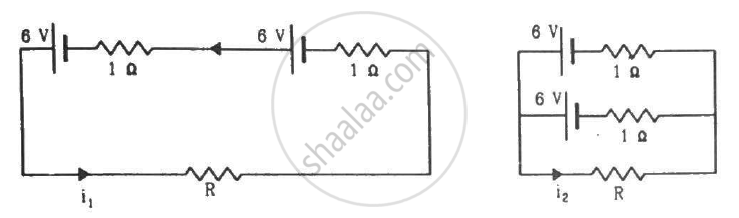
Find the value of i1/i2 in the following figure if (a) R = 0.1 Ω (b) R = 1 Ω and (c) R = 10 Ω. Note from your answers that in order to get more current from a combination of two batteries, they should be joined in parallel if the external resistance is small and in series if the external resistance is large, compared to the internal resistance.
A battery of emf 100 V and a resistor of resistance 10 kΩ are joined in series. This system is used as a source to supply current to an external resistance R. If R is not greater than 100 Ω, the current through it is constant up to two significant digits.
Find its value. This is the basic principle of a constant-current source.
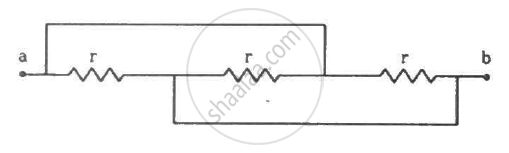
Find the equivalent resistance of the network shown in the figure between the points a and b.
The temperatures of the junctions of a bismuth-silver thermocouple are maintained at 0°C and 0.001°C. Find the thermo-emf (Seebeck emf) developed. For bismuth-silver, a = − 46 × 10−6 V°C−1 and b = −0.48 × 10−6 V°C−2.
A battery of EMF 10V sets up a current of 1A when connected across a resistor of 8Ω. If the resistor is shunted by another 8Ω resistor, what would be the current in the circuit? (in A)
Study the two circuits shown in the figure below. The cells in the two circuits are identical to each other. The resistance of the load resistor R is the same in both circuits.
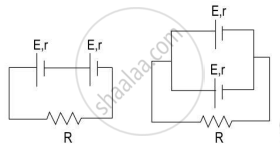
If the same current flows through the resistor R in both circuits, calculate the internal resistance of each cell in terms of the resistance of resistor R. Show your calculations.
