Advertisements
Advertisements
प्रश्न
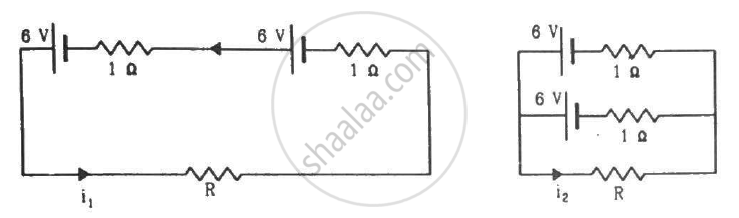
Find the value of i1/i2 in the following figure if (a) R = 0.1 Ω (b) R = 1 Ω and (c) R = 10 Ω. Note from your answers that in order to get more current from a combination of two batteries, they should be joined in parallel if the external resistance is small and in series if the external resistance is large, compared to the internal resistance.
उत्तर
(a) For R = 0.1 Ω
Applying KVL in the given circuit, we get:-
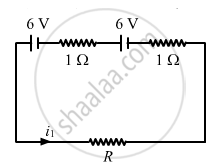
\[0 . 1 i_1 + 1 i_1 - 6 + 1 i_1 - 6 = 0\]
\[ \Rightarrow 0 . 1 i_1 + 1 i_1 + 1 i_1 = 12\]
\[ \Rightarrow i_1 = \frac{12}{\left( 2 . 1 \right)} = 5 . 71 A\]
Now, consider the given circuit.
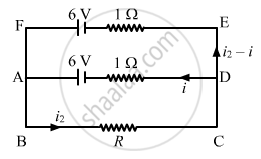
Applying KVL in the loop ABCDA, we get:-
\[0 . 1 i_2 + 1i - 6 = 0\]
\[ \Rightarrow 0 . 1 i_2 + i = 6\]
\[ \Rightarrow i = 6 - 0 . 1 i_2\]
Applying KVL in ADEFA, we get:-
\[i - 6 + 6 - \left( i_2 - i \right)1 = 0\]
\[ \Rightarrow i - i_2 + i = 0\]
\[ \Rightarrow 2i - i_2 = 0\]
\[ \Rightarrow 2\left[ 6 - 0 . 1 i_2 \right] - i_2 = 0\]
\[ \Rightarrow i_2 = 10 A\]
\[\therefore \frac{i_1}{i_2} = 0 . 571\]
(b) For R = 1 Ω
Applying KVL in the circuit given in figure 1, we get:-
\[1 i_1 + 1 . i_1 - 6 + i_1 - 6 = 0\]
\[ \Rightarrow 3 i_1 = 12\]
\[ \Rightarrow i_1 = 4\]
Now, for figure 2:-
Applying KVL in ABCDA, we get:-
\[i_2 + i - 6 = 0\]
\[ \Rightarrow i_2 + i = 6\]
Applying KVL in ADEFA, we get:-
\[i - 6 + 6 - \left( i_2 - i \right)1 = 0\]
\[ \Rightarrow i - i_2 + i = 0\]
\[ \Rightarrow 2i - i_2 = 0\]
\[ \Rightarrow 2\left[ 6 - i_2 \right] - i_2 = 0\]
\[ \Rightarrow 12 - 3 i_2 = 0\]
\[ \Rightarrow i_2 = 4 A\]
\[ \therefore \frac{i_1}{i_2} = 1\]
(c) For R = 10 Ω
Applying KVL in the circuit given in figure 1, we get:-
\[10 i_1 + 1 i_1 - 6 + 1 i_1 - 6 = 0\]
\[\Rightarrow 12 i_1 = 12\]
\[ \Rightarrow i_1 = 1\]
Now, for figure 2:-
Applying KVL in ABCDA, we get:-
\[10 i_2 + i - 6 = 0\]
\[ \Rightarrow i = 6 - 10 i_2\]
Applying KVL in ADEFA, we get:-
\[i - 6 + 6 - \left( i_2 - i \right)1 = 0\]
\[ \Rightarrow i - i_2 + i = 0\]
\[ \Rightarrow 2i - i_2 = 0\]
\[ \Rightarrow 2\left[ 6 - 10 i_2 \right] - i_2 = 0\]
\[ \Rightarrow 12 - 21 i_2 = 0\]
\[ \Rightarrow i_2 = 0 . 57 A\]
\[ \therefore \frac{i_1}{i_2} = 1 . 75\]
APPEARS IN
संबंधित प्रश्न
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4 Ω, what is the maximum current that can be drawn from the battery?
A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 Ω. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?
In a potentiometer arrangement for determining the emf of a cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9 Ω is used in the external circuit of the cell, the balance point shifts to 300 cm. Determine the internal resistance of the cell.
Plot a graph showing variation of voltage vs the current drawn from the cell. How can one get information from this plot about the emf of the cell and its internal resistance?
Two cells of emf E1, E2 and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure.

Deduce the expressions for
(1) the equivalent e.m.f of the combination
(2) the equivalent resistance of the combination, and
(3) the potential difference between the point A and B.
Consider N = n1n2 identical cells, each of emf ε and internal resistance r. Suppose n1 cells are joined in series to form a line and n2 such lines are connected in parallel.
The combination drives a current in an external resistance R. (a) Find the current in the external resistance. (b) Assuming that n1 and n2 can be continuously varied, find the relation between n1, n2, R and r for which the current in R is maximum.
Do the electrodes in an electrolytic cell have fixed polarity like a battery?
The temperatures of the junctions of a bismuth-silver thermocouple are maintained at 0°C and 0.001°C. Find the thermo-emf (Seebeck emf) developed. For bismuth-silver, a = − 46 × 10−6 V°C−1 and b = −0.48 × 10−6 V°C−2.
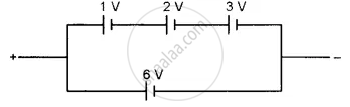
Find the emf of the battery shown in the figure:
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by ______.
Two batteries of emf ε1 and ε2 (ε2 > ε1) and internal resistances r1 and r2 respectively are connected in parallel as shown in figure.
A cell of emf E is connected across an external resistance R. When current 'I' is drawn from the cell, the potential difference across the electrodes of the cell drops to V. The internal resistance 'r' of the cell is ______.
Three cells, each of emf E but internal resistances 2r, 3r and 6r are connected in parallel across a resistor R.
Obtain expressions for (i) current flowing in the circuit, and (ii) the terminal potential differences across the equivalent cell.
Study the two circuits shown in the figure below. The cells in the two circuits are identical to each other. The resistance of the load resistor R is the same in both circuits.
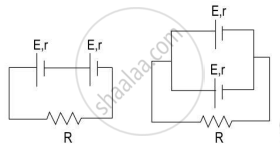
If the same current flows through the resistor R in both circuits, calculate the internal resistance of each cell in terms of the resistance of resistor R. Show your calculations.
